题目内容
已知:如图,正方形ABCD的边长为a,BM,DN分别平分正方形的两个外角,且满足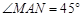 ,连结MC,NC,MN.
,连结MC,NC,MN.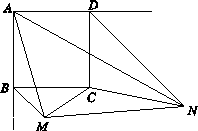
【小题1】(1)填空:与△ABM相似的三角形是△ ,
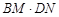 = ;(用含a的代数式表示)
= ;(用含a的代数式表示)【小题2】(2)求
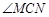 的度数;
的度数;【小题3】(3)猜想线段BM,DN和MN之间的等量关系并证明你的结论.

【小题1】(1)与△ABM相似的三角形是△NDA,

【小题2】(2)由(1)△ABM∽△NDA可得
 .………………3分
.………………3分∵ 四边形ABCD是正方形,
∴AB=DC,DA= BC,
 .
.∴
 .
.∵ BM,DN分别平分正方形ABCD的两个外角,
∴
 .
.∴△BCM∽△DNC.…………………………………………………………4分
∴
 .
.∴

 .
.【小题3】(3)线段BM,DN和MN之间的等量关系是
 .
.(只猜想答案不证明不给分)
证法一:如图9,将△AND绕点A顺时针旋转90°得到△ABF,连接MF.则
 △ABF≌△ADN.…………………………………………………6分
△ABF≌△ADN.…………………………………………………6分∴
 ,AF=AN,BF=DN,
,AF=AN,BF=DN, .
.∴
 .
.∴
 .
.又∵ AM= AM,
∴△AMF≌△AMN.
∴MF=MN.
可得
 .
.∴在Rt△BMF中,
 .
.∴
 .…………………………………………7分
.…………………………………………7分证法二:连接BD,作ME∥BD,与DN交于点E.(如图10)
可知
 ,
, .……………………………………6分
.……………………………………6分∵ ME∥BD,
∴
 .
.∵
 ,
,∴四边形BDEM是矩形.
∴ME=BD,BM=DE.
在Rt△MEN中,
 ,
,∴


 .解析:
.解析:略

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 ,连接DF,交BE的延长线于点G,连接OG.
,连接DF,交BE的延长线于点G,连接OG.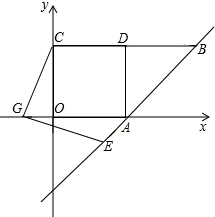
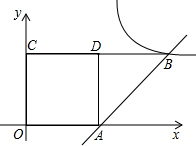
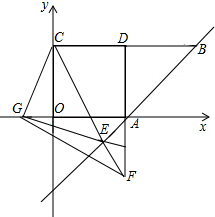



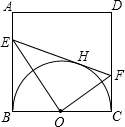 于E,交CD于F.
于E,交CD于F. 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.