题目内容
 如图,点C是线段AB的中点,点D,E在直线AB的同侧,∠ECA=∠DCB,∠D=∠E.
如图,点C是线段AB的中点,点D,E在直线AB的同侧,∠ECA=∠DCB,∠D=∠E.
求证:AD=BE.
证明:∵点C是线段AB的中点,
∴AC=BC,
∵∠ECA=∠DCB,
∴∠ECA+∠ECD=∠DCB+∠ECD,
即∠ACD=∠BCE,
∵在△ACD和△BCE中,
 ,
,
∴△ACD≌△BCE(AAS),
∴AD=BE.
分析:根据线段中点的定义可得AC=BC,然后求出∠ACD=∠BCE,再利用“角角边”证明△ACD和△BCE全等,然后利用全等三角形对应边相等证明即可.
点评:本题考查了全等三角形的判定与性质,比较简单,求出三角形全等的条件∠ACD=∠BCE是解题的关键.
∴AC=BC,
∵∠ECA=∠DCB,
∴∠ECA+∠ECD=∠DCB+∠ECD,
即∠ACD=∠BCE,
∵在△ACD和△BCE中,
 ,
,∴△ACD≌△BCE(AAS),
∴AD=BE.
分析:根据线段中点的定义可得AC=BC,然后求出∠ACD=∠BCE,再利用“角角边”证明△ACD和△BCE全等,然后利用全等三角形对应边相等证明即可.
点评:本题考查了全等三角形的判定与性质,比较简单,求出三角形全等的条件∠ACD=∠BCE是解题的关键.

练习册系列答案
相关题目
如图,点C是线段AB的中点,点D是线段BC的中点,下面等式不正确的是( )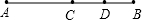
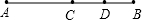
| A、CD=AD-BC | ||
| B、CD=AC-DB | ||
C、CD=
| ||
D、CD=
|
 10、如图,点D是线段AB与线段BC的垂直平分线的交点,∠B=40°,则∠ADC等于( )
10、如图,点D是线段AB与线段BC的垂直平分线的交点,∠B=40°,则∠ADC等于( )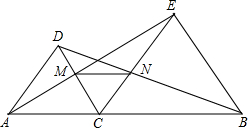 AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N. 如图,点C是线段AB的中点,点D是线段CB上任意一点,则下列表示线段关系的式子不正确的是( )
如图,点C是线段AB的中点,点D是线段CB上任意一点,则下列表示线段关系的式子不正确的是( ) 如图,点C是线段AB的中点,点D是线段BC的中点,则下列结论中错误的是( )
如图,点C是线段AB的中点,点D是线段BC的中点,则下列结论中错误的是( )