题目内容
【题目】已知直线l：y=kx+4与抛物线y=
x2交于点A(x1，y1)，B(x2，y2)．
(1)求：
；
的值．
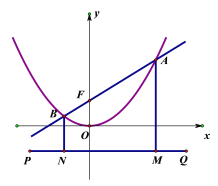
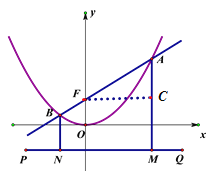
(2)过点(0，-4)作直线PQ∥x轴，且过点A、B分别作AM⊥PQ于点M，BN⊥PQ于点N，设直线l：y=kx+4交y轴于点F．求证：AF=AM=4+y1．
(3)证明：
+
为定值，并求出该值．
【答案】（1）
，
；（2）见解析；（3）
．
【解析】
（1）联立y=kx+4与y=
x2，根据一元二次方程根与系数的关系即可求出
、
的值；
（2）作FC⊥AM于点C，可求F（0,4）.设A（x1 x1）,根据勾股定理及图形与坐标的关系可证结论成立；
（3）求出AF=
， BF=
，代入
+
化简即可.
∵y=kx+4，y=x2，
∴x2- kx-4=0，
∴,
；
∵y1=kx1+4，y2=kx2+4，
∴
；
（2）作FC⊥AM于点C，
∵当x=0时，
y=0+4=4，
∴F（0,4）.
设A（x1 x12）,
∴AF=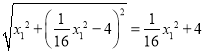
.
∵AM=
，
∴AF=AM.
∵y1=x12，
∴AF=AM=4+y1；
（3）由（2）知，AF=，同理可求BF=
.
∴+
=
=
= 
.
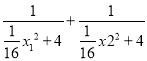
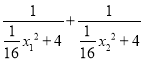
∵ y2+(-8-16k2)y+16=0,
∴，
，
∴+=
= 
.
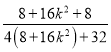
练习册系列答案
相关题目
【题目】某商店分两次购进
、
两种商品进行销售，两次购进同一种商品的进价相同，具体情况如下表所示：
购进数量（件） | 购进所需费用 （元） | ||
A | B | ||
第一次 | 20 | 50 | 4100 |
第二次 | 30 | 40 | 3700 |
（1）求、两种商品每件的进价分别是多少元？
（2）商场决定商品以每件50元出售，商品以每件
元出售．为满足市场需求，需购进、两种商品共
件，且商品的数量不少于商品数量的
倍，请你求出获利最大的进货方案，并确定最大利润．
