题目内容
 如图,AD⊥BC,垂足为D.如果CD=1,AD=3,BD=9,那么△ABC是直角三角形吗?请说明理由.
如图,AD⊥BC,垂足为D.如果CD=1,AD=3,BD=9,那么△ABC是直角三角形吗?请说明理由.
解:∵AD⊥BC,CD=1,AD=3,
∴AC2=CD2+AD2=10,
又∵AD⊥BC,AD=3,BD=9,
∴AB2=AD2+BD2=90,
∵BC=CD+BD=10,
∴BC2=100,
∴AC2+AB2=100=BC2,
∴△ABC是直角三角形.
分析:在Rt△ACD中利用勾股定理可求AC2,同理在Rt△ABD中利用勾股定理可求AB2,而BC=CD+BD=10,易求AC2+AB2=100=BC2,从而可知△ABC是直角三角形.
点评:本题考查勾股定理、勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
∴AC2=CD2+AD2=10,
又∵AD⊥BC,AD=3,BD=9,
∴AB2=AD2+BD2=90,
∵BC=CD+BD=10,
∴BC2=100,
∴AC2+AB2=100=BC2,
∴△ABC是直角三角形.
分析:在Rt△ACD中利用勾股定理可求AC2,同理在Rt△ABD中利用勾股定理可求AB2,而BC=CD+BD=10,易求AC2+AB2=100=BC2,从而可知△ABC是直角三角形.
点评:本题考查勾股定理、勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
相关题目
 4、如图,下列说法不正确的是( )
4、如图,下列说法不正确的是( )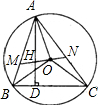 OB、OC,连接OH并延长交AB于M,交AC于N,求证:
OB、OC,连接OH并延长交AB于M,交AC于N,求证:

 如图,∠BAC=90°,AD⊥BC,则下列的结论中正确的个数是( )
如图,∠BAC=90°,AD⊥BC,则下列的结论中正确的个数是( )