题目内容
如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )
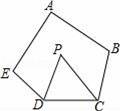

A.60° B.65° C.55° D.50°
A【考点】多边形内角与外角;三角形内角和定理.
【分析】根据五边形的内角和等于540°,由∠A+∠B+∠E=300°,可求∠BCD+∠CDE的度数,再根据角平分线的定义可得∠PDC与∠PCD的角度和,进一步求得∠P的度数.
【解答】解:∵五边形的内角和等于540°,∠A+∠B+∠E=300°,
∴∠BCD+∠CDE=540°﹣300°=240°,
∵∠BCD、∠CDE的平分线在五边形内相交于点O,
∴∠PDC+∠PCD=
 (∠BCD+∠CDE)=120°,
(∠BCD+∠CDE)=120°,
∴∠P=180°﹣120°=60°.
故选:A.
【点评】本题主要考查了多边形的内角和公式,角平分线的定义,熟记公式是解题的关键.注意整体思想的运用.

练习册系列答案
相关题目

 C.8 D.
C.8 D.
 =
= ,求
,求 的值.
的值.
 B.
B.
 C.
C.
 D.
D.


 有意义的x的取值范围是 .
有意义的x的取值范围是 .
 ?若存在求出x的值;若不存在请说明理由.
?若存在求出x的值;若不存在请说明理由.