题目内容
 如图:∠AOB:∠BOC:∠COD=2:3:4,射线OM、ON分别平分∠AOB与∠COD,又∠MON=90°,则∠AOB为
如图:∠AOB:∠BOC:∠COD=2:3:4,射线OM、ON分别平分∠AOB与∠COD,又∠MON=90°,则∠AOB为
- A.20°
- B.30°
- C.40°
- D.45°
B
分析:首先设出未知数,然后利用角的和差关系和角平分线的性质列出方程,即可求出∠AOB的度数.
解答:设∠AOB=2x°则∠BOC=3x°∠COD=4x°,
∵射线OM、ON分别平分∠AOB与∠COD,
∴∠BOM= ∠AOB=x°,
∠AOB=x°,
∠CON= ∠COD=2x°,
∠COD=2x°,
又∵∠MON=90°,
∴x+3x+2x=90,
x=15,
∴∠AOB=15°×2=30°.
故选B.
点评:本题主要考查了角平分线的性质和角的和差关系,解题时要能根据图形找出等量关系列出方程,求出角的度数.
分析:首先设出未知数,然后利用角的和差关系和角平分线的性质列出方程,即可求出∠AOB的度数.
解答:设∠AOB=2x°则∠BOC=3x°∠COD=4x°,
∵射线OM、ON分别平分∠AOB与∠COD,
∴∠BOM=
 ∠AOB=x°,
∠AOB=x°,∠CON=
 ∠COD=2x°,
∠COD=2x°,又∵∠MON=90°,
∴x+3x+2x=90,
x=15,
∴∠AOB=15°×2=30°.
故选B.
点评:本题主要考查了角平分线的性质和角的和差关系,解题时要能根据图形找出等量关系列出方程,求出角的度数.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
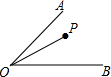 如图,∠AOB=45°,点P为∠AOB内一点,且OP=4,M为OA上一点,N为OB上一点,则△PMN的周长的最小值为( )
如图,∠AOB=45°,点P为∠AOB内一点,且OP=4,M为OA上一点,N为OB上一点,则△PMN的周长的最小值为( )A、4
| ||
B、4
| ||
| C、4 | ||
D、2
|
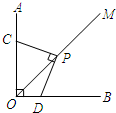 如图,∠AOB=90°,OM是∠AOB的平分线,将三角尺的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于点C和D,证明:PC=PD.
如图,∠AOB=90°,OM是∠AOB的平分线,将三角尺的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于点C和D,证明:PC=PD. 如图,∠AOB是一建筑钢架,∠AOB=10°,为使钢架更加稳固,需在内部添加一些钢管EF、FG、GH、HI、IJ,添加钢管的长度都与OE相等,则∠BIJ=( )
如图,∠AOB是一建筑钢架,∠AOB=10°,为使钢架更加稳固,需在内部添加一些钢管EF、FG、GH、HI、IJ,添加钢管的长度都与OE相等,则∠BIJ=( )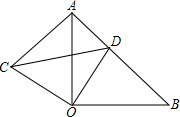 如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上.
如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上. 如图,AOB是一条直线,∠AOD=∠COE=90°,则图中∠1的余角是
如图,AOB是一条直线,∠AOD=∠COE=90°,则图中∠1的余角是