题目内容
（2013•临沂）如图，等腰梯形ABCD中，AD∥BC，DE⊥BC，BD⊥DC，垂足分别为E，D，DE=3，BD=5，则腰长AB=| 15 |
| 4 |
| 15 |
| 4 |
分析：利用勾股定理列式求出BE的长，再利用∠CBD的正切值列式求出CD，然后根据等腰梯形的腰长相等解答．
解答：解：∵DE=3，BD=5，DE⊥BC，
∴BE=
=
=4，
又∵BD⊥DC，
∴tan∠CBD=
=
，
即
=
，
解得CD=
，
∵梯形ABCD是等腰梯形，AD∥BC，
∴AB=CD=
．
故答案为：
．
∴BE=
| BD2-DE2 |
| 52-32 |
又∵BD⊥DC，
∴tan∠CBD=
| CD |
| BD |
| DE |
| BE |
即
| CD |
| 5 |
| 3 |
| 4 |
解得CD=
| 15 |
| 4 |
∵梯形ABCD是等腰梯形，AD∥BC，
∴AB=CD=
| 15 |
| 4 |
故答案为：
| 15 |
| 4 |
点评：本题考查了等腰梯形的两腰相等，勾股定理的应用，利用锐角三角函数求解更加简便．
练习册系列答案
相关题目
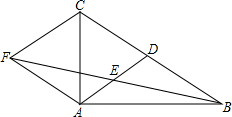（2013•临沂）如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．
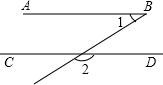（2013•临沂）如图，已知AB∥CD，∠2=135°，则∠1的度数是（ ）
（2013•临沂）如图，四边形ABCD中，AC垂直平分BD，垂足为E，下列结论不一定成立的是（ ）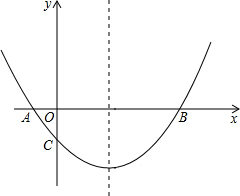
（2013•临沂）如图，抛物线经过A（-1，0），B（5，0），C（0，