题目内容
已知在△ABC中，E为AC的中点，延长BC到D使DC=BC，连结DE并延长交AB于F，求证：ED=3EF．
考点：平行线分线段成比例,三角形中位线定理
专题：证明题
分析：先画出图形，过点E作EG∥AB，交BC与点G，得出
=
，再根据E为AC的中点，得出BC=2BG，再根据DC=BC，得出DG=3BG，即可证出结论．
| DG |
| BG |
| DE |
| EF |
解答：
解；如图：过点E作EG∥AB，交BC与点G，
则
=
，
∵E为AC的中点，
∴BG=CG，
∴BC=2BG，
∵DC=BC，
∴DC=2BG，
∴DG=3BG，
∴
=
=3，
∴ED=3EF．
解；如图：过点E作EG∥AB，交BC与点G，则
| DG |
| BG |
| DE |
| EF |
∵E为AC的中点，
∴BG=CG，
∴BC=2BG，
∵DC=BC，
∴DC=2BG，
∴DG=3BG，
∴
| DG |
| BG |
| DE |
| EF |
∴ED=3EF．
点评：此题主要考查平行线分线段成比例定理的理解及运用，关键是根据题意画出图形做出辅助线，找出成比例的线段．
练习册系列答案
相关题目
a、b在的位置如图所示，则数a、-a、b、-b的大小关系为
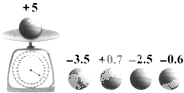如图，检测5个排球，其中超过标准的克数记为正数，不足的克数记为负数．从轻重的角度看，哪个球最接近标准？（ ）| A、-3.5 | B、+0.7 |
| C、-2.5 | D、-0.6 |
如果a＞0，b＜0，且|a|＞|b|，那么|a+b|等于（ ）
| A、a-b | B、a+b |
| C、b-a | D、-a-b |