题目内容
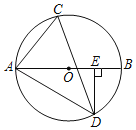
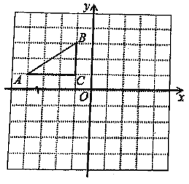
【题目】如图,等腰![]() 中,
中, ![]() ,点
,点![]() 是
是![]() 边上一点,在
边上一点,在![]() 上取点
上取点![]() ,使
,使![]()
(1)求证: ![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)利用三角形外角定理证得∠EDC=∠DAB,再根据两角相等即可证明△ABD∽△DCE;
(2)作高AF,利用三角函数求得![]() ,继而求得
,继而求得![]() ,再根据△ABD∽△DCE,利用对应边成比例即可求得答案.
,再根据△ABD∽△DCE,利用对应边成比例即可求得答案.
(1)∵△ABC是等腰三角形,且∠BAC=120°,
∴∠ABD=∠ACB=30°,
∴∠ABD=∠ADE=30°,
∵∠ADC=∠ADE+∠EDC=∠ABD+∠DAB,
∴∠EDC=∠DAB,
∴△ABD∽△DCE;
(2)过![]() 作
作![]() 于
于![]() ,
,

∵△ABC是等腰三角形,且∠BAC=120°,![]() ,
,
∴∠ABD=∠ACB=30°,![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
所以![]() .
.

【题目】为了解学生每天的睡眠情况,某初中学校从全校 800 名学生中随机抽取了 40 名学生,调查了他们平均每天的睡眠时间(单位: h) ,统计结果如下:
9,8,10.5,7,9,8,10,9.5,8,9,9.5,7.5,9.5,9,8.5,7.5,10,9.5,8,9,
7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9.
在对这些数据整理后,绘制了如下的统计图表:
睡眠时间分组统计表 睡眠时间分布情况
组别 | 睡眠时间分组 | 人数(频数) |
1 | 7≤t<8 | m |
2 | 8≤t<9 | 11 |
3 | 9≤t<10 | n |
4 | 10≤t<11 | 4 |

请根据以上信息,解答下列问题:
(1) m = , n = , a = , b = ;
(2)抽取的这 40 名学生平均每天睡眠时间的中位数落在 组(填组别) ;
(3)如果按照学校要求,学生平均每天的睡眠时间应不少于 9 h,请估计该校学生中睡眠时间符合要求的人数.
【题目】某市水费采用阶梯收费制度,即:每月用水不超过15吨时,每吨需缴纳水费a元,每月用水量超过15吨时,超过15吨的部分按每吨提高b元缴纳下表是嘉琪家一至四月份用水量和缴纳水费情况.根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
月用水量(吨) | 14 | 18 | 16 | 13 |
水费(元) | 42 | 60 | 50 | 39 |
(1)a= 元;b= 元;
(2)求月缴纳水费p(元)与月用水量t(吨)之间的函数关系式;
(3)若嘉琪家五月和六月的月缴水费相差24元,求这两月用水量差的最小值.