题目内容
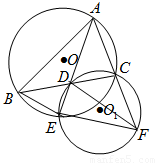
如图, 是
是 的角平分线, 延长
的角平分线, 延长 交
交 的外接圆
的外接圆 于点
于点 ,过
,过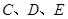 三点的圆
三点的圆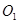 交
交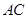 的延长线于点
的延长线于点 ,连结
,连结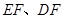 .
.
(1)求证: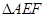 ∽
∽ ;
;
(2) 若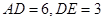 , 求
, 求 的长;
的长;
(3) 若 ∥
∥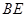 , 试判断
, 试判断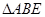 的形状,并说明理由.
的形状,并说明理由.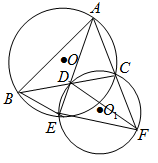
(1)证明:连结两圆的相交弦
在圆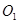 中,
中, ,
,
在圆 中,
中, ,
,
∴ ,
,
又因为 是
是 角平分线,得∠BAE=∠CAE,
角平分线,得∠BAE=∠CAE,
∴ ,
,
∵ ,
,
∴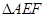 ∽
∽ .
.
(2)∵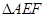 ∽
∽ ,
,
∴ ,
,
∴ ,
,
∴ .
.
(3)证明:根据同弧上的圆周角相等,
得到: ,
, ,
,
∴ ,
,
∵ =180°,
=180°,
∴ =180°,
=180°,
又 =180,
=180,
∴ .
.
∵ ∥
∥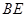 ,
, ,
,
又∵ ,
,
∴∠AEB =∠ABE ,
∴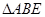 为等腰三角形.
为等腰三角形.
解析

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目

 是
是 的角平分线,
的角平分线, ∥
∥ ,如果
,如果 ,那么
,那么


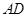 是
是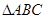 的角平分线, 延长
的角平分线, 延长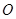 于点
于点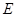 ,过
,过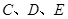 三点的圆
三点的圆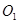 交
交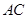 的延长线于点
的延长线于点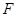 ,连结
,连结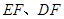 .
.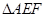 ∽
∽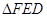 ;
;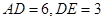 , 求
, 求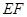 的长;
的长;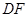 ∥
∥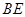 , 试判断
, 试判断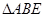 的形状,并说明理由.
的形状,并说明理由.