题目内容
在□ABCD中,E、F分别是AB、CD的中点,连接AF、CE.

1.求证:△BEC≌△DFA;
2.连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论
1.因为四边形ABCD是平行四边形,所以 ,
,
BC=DA,又因为BE=DF,所以△BEC≌△DFA;
4分
2.矩形
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AE=CF,
∴四边形AECF是平行四边形,
∵AC=BC,E是AB的中点,
∴CE⊥AB,
∴∠AEC=90°,
∴平行四边形AECF是矩形. 5分
解析:本题考查平行四边形的性质和矩形的判定。难度不大。

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
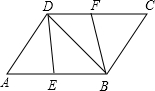 如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD. 如图,在?ABCD中,EF∥AB,MN∥BC,MN与EF交于点O,且O点在对角线上,图中面积相等的四边形有( )
如图,在?ABCD中,EF∥AB,MN∥BC,MN与EF交于点O,且O点在对角线上,图中面积相等的四边形有( )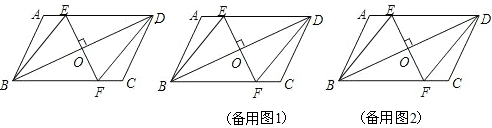
 如图,在?ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.
如图,在?ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.