Question

【题目】(1)问题引入：如图1所示，正方形和正方形，则与的数量关系是 ， ；

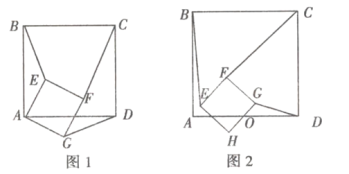
(2)类比探究：如图2所示，为、的中点，正方形和正方形中，判断和的数量关系，并求出的值．

(3)解决问题：

①若把(1)中的正方形都改成矩形，且，则(1)中的结论还成立吗?若不能成立，请写出与的关系，并求出的值；

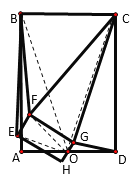
②若把(2)中的正方形也都改成矩形，且，请直接写出和的关系以及的值．

Answer 1

【答案】(1) ；(2) ，理由见解析；(3)①结论不成立．此时．理由见解析；②．

【解析】

（1）根据SAS证明△ABE≌△ADG即可得到BE=DG，连接AC、AF，证明△CAF∽△DAG，即可得到；

（2）连接，证明△EOH≌△FOG得到，再证明，得到，得到BE=FC，再证明即可求出；

（3）①证明得到BE=3DG，连接，根据tan∠FAG=tan∠CAD=3，证明，根据证明，得到；

②连接，证明△EOH≌△FOG得到，再证明，得到，得到BE=FC，再证明即可求出.

(1) ∵四边形ABCD与四边形AEFG都是正方形，

∴AB=AD，AE=AG，∠BAD=∠EAG=90°，

∴∠BAD-∠EAD=∠EAG-∠EAD,

即∠BAE=∠DAG,

∴△ABE≌△ADG，

∴BE=DG，

连接AC、AF，则， ,

∵∠CAD=∠FAG=45°，

∴∠CAD-∠FAD=∠FAG-∠FAD,

∴∠CAF=∠DAG，

∴△CAF∽△DAG，

∴

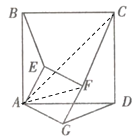
(2).

理由如下：连接

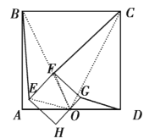
∵正方形是中点，

.

.

.

同理：

又，

.

.

.

.

.

又，

，

又

(3)①结论不成立.此时.

理由如下：由题可得，

.

又

.

.

连接

，

.

又，

.

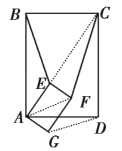
②,

理由如下：连接,

∵矩形是中点，

.

.

.

同理：

又 ，

.

.

.

.

.

又，

，

∵，

∴，

∴，

∵AB=CD，

∴，

又，

，

，

.