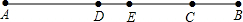题目内容
如图，M是线段AC的中点，N是线段BC的中点．
（1）如果AC=8cm，BC=6cm，求MN的长．
（2）如果AM=5cm，CN=2cm，求线段AB的长．
解：（1）∵M是AC的中点，N是BC的中点，
∴MN=MC+CN=
AC+BC=AB=7cm．
则MN=7cm．
（2）∵M是线段AC的中点，N是线段BC的中点，
若AM=5cm，CN=2cm，
∴AB=AC+BC=10+4=14cm．
分析：（1）因为M是AC的中点，N是BC的中点，则MC=AC，CN=BC，故MN=MC+CN可求；
（2）根据中点的概念，分别求出AC、BC的长，然后求出线段AB．
点评：本题主要考查两点间的距离的知识点，能够根据中点的概念，用几何式子表示线段的关系，还要注意线段的和差表示方法．
∴MN=MC+CN=
AC+BC=AB=7cm．则MN=7cm．
（2）∵M是线段AC的中点，N是线段BC的中点，
若AM=5cm，CN=2cm，
∴AB=AC+BC=10+4=14cm．
分析：（1）因为M是AC的中点，N是BC的中点，则MC=
AC，CN=BC，故MN=MC+CN可求；（2）根据中点的概念，分别求出AC、BC的长，然后求出线段AB．
点评：本题主要考查两点间的距离的知识点，能够根据中点的概念，用几何式子表示线段的关系，还要注意线段的和差表示方法．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
2、如图，B是线段AC的中点，过点C的直线l与AC成60°的角，在直线L上取一点P，使∠APB=30°，则满足条件的点P的个数是（ ）
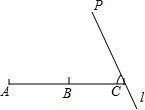如图，B是线段AC的中点，过点C的直线l与AC成50°的角，在直线l上取一点P，使得∠APB=30°，则满足条件的点P的个数是（ ）| A、1个 | B、2个 | C、3个 | D、无数个 |
如图，M是线段AC的中点，N是线段CB的中点．
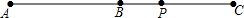如图，B是线段AC的中点，P是BC上一点，若PA=a，PC=b，则线段PB的长是（ ）| A、a-b | ||
B、
| ||
| C、2a-3b | ||
D、
|