题目内容
【题目】如图,在直线y= ![]() x+1上取一点A1 , 以O、A1为顶点作等一个等边三角形OA1B1 , 再在直线上取一点A2 , 以A2、B1为顶点作第二个等边三角形A2B1B2 , …,一直这样做下去,则B1点的坐标为 , 第10个等边三角形的边长为 .
x+1上取一点A1 , 以O、A1为顶点作等一个等边三角形OA1B1 , 再在直线上取一点A2 , 以A2、B1为顶点作第二个等边三角形A2B1B2 , …,一直这样做下去,则B1点的坐标为 , 第10个等边三角形的边长为 . 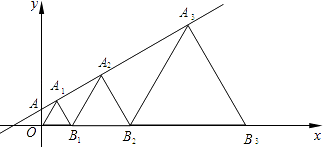
【答案】( ![]() ;0);29
;0);29 ![]()
【解析】解:作A1D⊥x轴于D,A2E⊥x轴于E,如图,

∵△OA1B1、△B1A2B2均为等边三角形,
∴OD=B1D,B1E=B2E,∠OA1D=30°,∠B1A2E=30°,
设OD=t,B1E=a,则A1D= ![]() t,A2E=
t,A2E= ![]() a,
a,
∴A1点坐标为(t, ![]() t),
t),
把A1(t, ![]() t)代入y=
t)代入y= ![]() x+1得
x+1得 ![]() t=
t= ![]() t+1,解得t=
t+1,解得t= ![]() ,
,
∴OB1= ![]() ,
,
∴B1点的坐标为( ![]() ,0),
,0),
∴A2点坐标为( ![]() +a,
+a, ![]() a),
a),
把A2( ![]() +a,
+a, ![]() a)代入y=
a)代入y= ![]() x+1得
x+1得 ![]() a=
a= ![]() (
( ![]() +a)+1,解得a=
+a)+1,解得a= ![]() ,
,
∴B1B2=2 ![]() ,
,
同理得到B2B3=22 ![]() ,…,按照此规律得到B9B10=29
,…,按照此规律得到B9B10=29 ![]() .
.
所以答案是( ![]() ,0),29
,0),29 ![]() .
.

练习册系列答案
相关题目