题目内容
已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.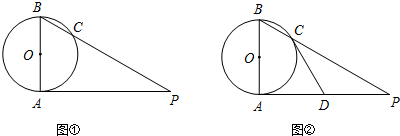
(1)如图①,若AB=2,∠P=30°,求AP的长(结果保留根号);
(2)如图②,若D为AP的中点,求证直线CD是⊙O的切线.
(1)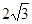 (2)证明OC⊥CD,得直线CD是⊙O的切线
(2)证明OC⊥CD,得直线CD是⊙O的切线
解析试题分析:(1)AP是⊙O的切线,AB是⊙O的直径,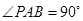 ;在
;在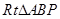 中由三角函数的定义得
中由三角函数的定义得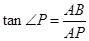 ,又因为AB=2,∠P=30°,所以
,又因为AB=2,∠P=30°,所以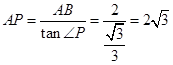
(2)连接OC、OD,如图所示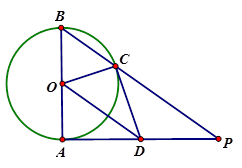
由题知OB=OC,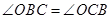 ;AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,
;AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,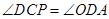 ;AB是⊙O的直径,O是AB的中点,若D为AP的中点,所以OD是
;AB是⊙O的直径,O是AB的中点,若D为AP的中点,所以OD是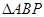 的中位线,则OD//BP,
的中位线,则OD//BP,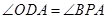 ,所以
,所以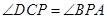 ;AP是⊙O的切线,AB是⊙O的直径,
;AP是⊙O的切线,AB是⊙O的直径,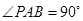 ,所以
,所以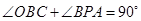 ,
,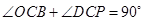 ,则
,则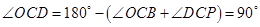 ,因此OC⊥CD,所以直线CD是⊙O的切线
,因此OC⊥CD,所以直线CD是⊙O的切线
考点:三角函数、直线与圆相切
点评:本题考查三角函数、直线与圆相切,要求考生掌握三角函数的定义,并利用它的定义来解题;掌握直线与圆的性质,会判定直线与圆相切

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
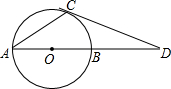 如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD=
如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD=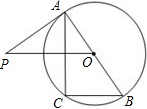 如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.
如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.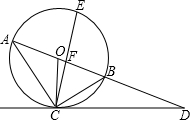

 如图,已知AB是⊙O的直径,AD切⊙O于点A,
如图,已知AB是⊙O的直径,AD切⊙O于点A,