题目内容
 如图,已知点A是一次函数y=2x的图象与反比例函数y=-
如图,已知点A是一次函数y=2x的图象与反比例函数y=- 的图象在第一象限内的交点,AB⊥x轴于点B,点C在x轴的负半轴上,且∠ACB=∠OAB,△AOB的面积为4,则点C的坐标为
的图象在第一象限内的交点,AB⊥x轴于点B,点C在x轴的负半轴上,且∠ACB=∠OAB,△AOB的面积为4,则点C的坐标为
- A.(-5,0)
- B.(-6,0)
- C.(-5.5,0)
- D.(-4,0)
B
分析:利用△AOB的面积为4即可求得k=-8,然后解方程组 得到A点坐标,即OB,AB的长,再由∠ACB=∠OAB得到Rt△BAO∽Rt△BCA,利用三角形相似的性质得OB:BA=BA:BC,即2:4=4:BC,求出BC,得到OC,从而确定C点坐标.
得到A点坐标,即OB,AB的长,再由∠ACB=∠OAB得到Rt△BAO∽Rt△BCA,利用三角形相似的性质得OB:BA=BA:BC,即2:4=4:BC,求出BC,得到OC,从而确定C点坐标.
解答:设A点坐标为(a,b),
∵△AOB的面积为4,
∴ ab=4,即ab=8,
ab=4,即ab=8,
而点A在反比例函数y=- 的图象上,
的图象上,
∴k=-ab=-8,即y= ,
,
解方程组 ,
,
解得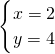 ,
,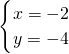 ,
,
∴A点坐标为(2,4);
又∵∠ACB=∠OAB,
∴Rt△BAO∽Rt△BCA,
∴OB:BA=BA:BC,即2:4=4:BC,
∴BC=8,
∴OC=6,
∴C点坐标为(-6,0).
故选B.
点评:本题考查了有关反比例函数的综合题:利用几何性质得到反比例函数的解析式,再建立两函数的解析式得到它们函数图象的交点坐标,从而得到有关线段的长,然后利用三角形相似的性质求其他相关线段的长.
分析:利用△AOB的面积为4即可求得k=-8,然后解方程组
 得到A点坐标,即OB,AB的长,再由∠ACB=∠OAB得到Rt△BAO∽Rt△BCA,利用三角形相似的性质得OB:BA=BA:BC,即2:4=4:BC,求出BC,得到OC,从而确定C点坐标.
得到A点坐标,即OB,AB的长,再由∠ACB=∠OAB得到Rt△BAO∽Rt△BCA,利用三角形相似的性质得OB:BA=BA:BC,即2:4=4:BC,求出BC,得到OC,从而确定C点坐标.解答:设A点坐标为(a,b),
∵△AOB的面积为4,
∴
 ab=4,即ab=8,
ab=4,即ab=8,而点A在反比例函数y=-
 的图象上,
的图象上,∴k=-ab=-8,即y=
 ,
,解方程组
 ,
,解得
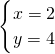 ,
,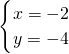 ,
,∴A点坐标为(2,4);
又∵∠ACB=∠OAB,
∴Rt△BAO∽Rt△BCA,
∴OB:BA=BA:BC,即2:4=4:BC,
∴BC=8,
∴OC=6,
∴C点坐标为(-6,0).
故选B.
点评:本题考查了有关反比例函数的综合题:利用几何性质得到反比例函数的解析式,再建立两函数的解析式得到它们函数图象的交点坐标,从而得到有关线段的长,然后利用三角形相似的性质求其他相关线段的长.

练习册系列答案
相关题目
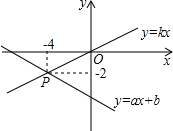 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x,y的二元一次方程组
如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x,y的二元一次方程组 六个面上分别标有1,1,2,3,3,5六个数字的均匀立方体的表面如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内的一个点的坐标.已知小明前两次掷得的两个点能确定一条直线,且这条直线经过点P(4,7),那么他第三次掷得的点也在直线上的概率是( )
六个面上分别标有1,1,2,3,3,5六个数字的均匀立方体的表面如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内的一个点的坐标.已知小明前两次掷得的两个点能确定一条直线,且这条直线经过点P(4,7),那么他第三次掷得的点也在直线上的概率是( ) 你结合这个新的图象回答:当直线y=x+m(m<1)与此图象有两个公共点时,m的取值范围是什么?
你结合这个新的图象回答:当直线y=x+m(m<1)与此图象有两个公共点时,m的取值范围是什么? 如图,已知函数y=ax+b和y=kx的图象交于点P,则二元一次方程组
如图,已知函数y=ax+b和y=kx的图象交于点P,则二元一次方程组