题目内容
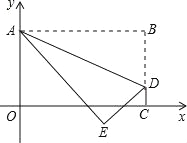
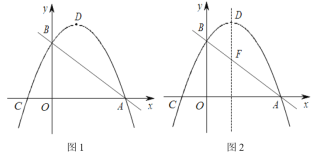
【题目】如图1,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点B;抛物线
与x轴交于点A,与y轴交于点B;抛物线![]() (a≠0)过A,B两点,与x轴交于另一点C(-1,0),抛物线的顶点为D.
(a≠0)过A,B两点,与x轴交于另一点C(-1,0),抛物线的顶点为D.
(1)求抛物线的解析式;
(2)在直线AB上方的抛物线上有一动点E,求出点E到直线AB的距离的最大值;
(3)如图2,直线AB与抛物线的对称轴相交于点F,点P在坐标轴上,且点P到直线 BD,DF的距离相等,请直接写出点P的坐标.
【答案】(1)![]() ;(2)E到直线AB的距离的最大值为
;(2)E到直线AB的距离的最大值为![]() ;(3)点P的坐标为:(0,1),(
;(3)点P的坐标为:(0,1),(![]() ,0),(0,
,0),(0,![]() ),(7,0).
),(7,0).
【解析】
(1)由一次函数![]() 求出点A,B的坐标,再将A,C坐标代入
求出点A,B的坐标,再将A,C坐标代入![]() 中即可解答;
中即可解答;
(2)通过证明△ENM∽△AOB,得到EN=![]() ,设E(m,
,设E(m,![]() ),M(m,
),M(m,![]() ),表达出EM,再由二次函数的性质求出最大值;
),表达出EM,再由二次函数的性质求出最大值;
(3)分当点P在∠BDF平分线上、外角平分线上两种情况,分别求解即可.
解:(1)在![]() 中,当x=0时,y=
中,当x=0时,y=![]() ;当y=0时,x=3,
;当y=0时,x=3,
即A(3,0),B(0,![]() ),
),
将A(3,0),C(-1,0)代入![]() 得:
得:
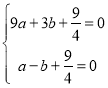 ,解得:
,解得: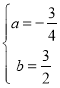 ,
,
∴抛物线的解析式为:![]() .
.
(2)过点E作EM⊥x轴交AB于M,过E作EN⊥AB于N,
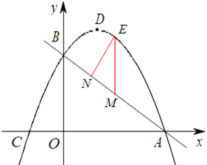
点E到AB的距离为EN,
∵EM∥y轴,
∴∠EMN=∠OBA,
又∵∠ENM=∠AOB,
∴△ENM∽△AOB,
∴![]() ,
,
在Rt△AOB中,OA=3,OB=![]() ,
,
由勾股定理得:AB=![]() ,
,
∴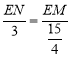 ,
,
即EN=![]() ,
,
设E(m,![]() ),M(m,
),M(m,![]() ),
),
则EM=![]() -(
-(![]() )=
)=![]() ,
,
∴EN=![]()
=![]()
=![]() ,
,
∴当m=![]() 时,E到直线AB的距离的最大值为
时,E到直线AB的距离的最大值为![]() .
.
(3)∵点P到直线BD,DF的距离相等,
∴点P在∠BDF或∠BDF邻补角的平分线上,如图所示,
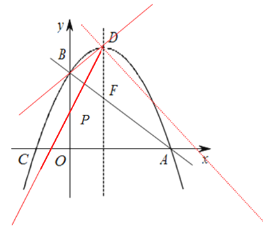
由![]() ,则 D点坐标为(1,3),
,则 D点坐标为(1,3),
∵B(0,![]() ),
),
∴BD=![]() ,
,
∵DP平分∠BDF,
∴∠BDP=∠PDF,
∵DF∥y轴,
∴∠BPD=∠PDF,
∴∠BPD=∠BDP,
∴BD=BP,
∴P(0,1),
设直线PD的解析式为:y=kx+n,
∴n=1,k+n=3,
即直线PD的解析式为:y=2x+1,
当y=0时,x=![]() ,
,
∴当P在∠BDF的角平分线上时,坐标为(0,1)或(![]() ,0);
,0);
同理可得:当P在∠BDF邻补角的平分线上时,坐标为:(0,![]() )或(7,0),
)或(7,0),
综上所述,点P的坐标为:(0,1),(![]() ,0),(0,
,0),(0,![]() ),(7,0).
),(7,0).

 名校课堂系列答案
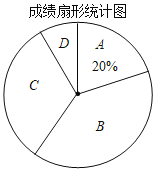
名校课堂系列答案【题目】在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整):
成绩频数分布统计表
组别 | A | B | C | D |
成绩x(分) | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
人数 | 10 | m | 16 | 4 |
请观察上面的图表,解答下列问题:
(1)统计表中m= ,D组的圆心角为 °;
(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求:
①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.