题目内容
 已知,如图:四边形ABCD中,∠C>90°,CD⊥AD于D,CB⊥AB于B,AB=
已知,如图:四边形ABCD中,∠C>90°,CD⊥AD于D,CB⊥AB于B,AB=| 3 |
| 3 |
| 1 |
| 4 |
(1)求tanA;
(2)若CD=m,求BC的值.
分析:(1)根据根的判别式可得m的值,进而解方程可得tanA的值;
(2)由(1)易得∠A的度数,延长四边形的两边,构造一个直角三角形,利用特殊角的三角函数计算即可.
(2)由(1)易得∠A的度数,延长四边形的两边,构造一个直角三角形,利用特殊角的三角函数计算即可.
解答:解:(1)∵关于x的方程x2-2
x+
(m2-2m+13)=0,
有实数根,∴△=(2
)2-4×
(m2-2m+13)≥0(2分)
整理得:-(m-1)2≥0(3分)
∴m=1(4分)
∴x2-2
x+3=0,
(x-
)2=0,
x1=x2=
∴tanA=
(5分)
(2)延长BC交AD的延长线于M,

由(1)得:tanA=
,m=1
∵CD⊥AD于D,CB⊥AB于B,∠C>90°,
∴∠A=60°(6分)
又CD=m=1
∴在RT△CDM中,∠M=30°
∴CM=2,DM=
(7分)
在RT△ABM中,∠M=30°
∵AB=
,
∴AM=2
∴AD=
,BM=3(9分)
∴BC=3-CM=3-2=1(10分).
| 3 |
| 1 |
| 4 |
有实数根,∴△=(2
| 3 |
| 1 |
| 4 |
整理得:-(m-1)2≥0(3分)
∴m=1(4分)
∴x2-2
| 3 |
(x-
| 3 |
x1=x2=
| 3 |
∴tanA=
| 3 |
(2)延长BC交AD的延长线于M,

由(1)得:tanA=
| 3 |
∵CD⊥AD于D,CB⊥AB于B,∠C>90°,
∴∠A=60°(6分)
又CD=m=1
∴在RT△CDM中,∠M=30°
∴CM=2,DM=
| 3 |
在RT△ABM中,∠M=30°
∵AB=
| 3 |
∴AM=2
| 3 |
∴AD=
| 3 |
∴BC=3-CM=3-2=1(10分).
点评:综合考查了解一元二次方程及三角函数的知识;把四边形转化为三角形解决问题是常用的解题方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
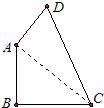 已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.
已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.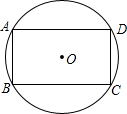 已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC,
已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC, 已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF
已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF 已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少?
已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少? 已知:如图,四边形ABCD及一点P.
已知:如图,四边形ABCD及一点P.