Question

一个正三角形和一个正六边形的面积相等，则它们的边长比为（　　）

• A、

  6

  ﹕1
• B、

  3

  ﹕1
• C、

  3

  3

  ﹕1
• D、

  2

  ﹕1

Answer 1

分析：根据题意画出图形，分别设出边长并表示出面积后即可利用面积相等得到答案．

解答：解：设正三角形的边长为a，则正六边形的边长为b；
（1）过A作AD⊥BC于D，则∠BAD=30°，

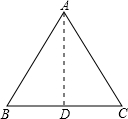
AD=AB•cos30°=a•

3

2

=

3

2

a，
∴S_△ABC=

1

2

BC•AD=

1

2

×a×

3

2

a=

3

4

a²；

（2）连接OA、OB，过O作OD⊥AB；

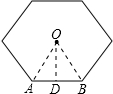
∵∠AOB=

360°

6

=60°，
∴∠AOD=30°，
OD=

AD

tan30°

=

b 2

3 3

=

3

2

b，
∴S_△OAB=

1

2

×b×

3

2

b=

3

4

b2，
∴S_六边形=6S_△OAB=6×

3 b2

4

=

3 3 b2

2

，
∵S_△ABC=S_六边形
∴

3 a2

4

=

3 3 b2

2

解得：a：b=

6

：1
故选A．

点评：本题考查了正三角形及正六边形的性质，解答此题的关键是根据题意画出图形，结合正多边形的性质解答．