题目内容
如图，P1、P2是函数
（x＞0）上的点，若△P1OA1、△P2A1A2是等腰直角三角形，斜边OA1、A1A2都在x轴上，则点P2的坐标是________．
（
+1，-1）
分析：根据P1的横纵坐标相等可得P1的坐标，设P2的纵坐标为a，代入反比例函数，可得相应坐标．
解答：∵P1为等腰直角三角形的顶点，
∴设P1的坐标为（x，x），
∴x2=1，
∵P1在第一象限，
∴x=1，
设P2的坐标为（2+a，a），
∴（2+a）a=1，
a2+2a-1=0，
解得a=-1±
∵a＞0，
∴a=-1，
∴P2（+1，-1）．
故答案为：（+1，-1）．
点评：此题主要考查了反比例函数比例系数k的意义的应用；判断出所求坐标的横纵坐标的代数式是解决本题的关键．
+1，-1）分析：根据P1的横纵坐标相等可得P1的坐标，设P2的纵坐标为a，代入反比例函数，可得相应坐标．
解答：∵P1为等腰直角三角形的顶点，
∴设P1的坐标为（x，x），
∴x2=1，
∵P1在第一象限，
∴x=1，
设P2的坐标为（2+a，a），
∴（2+a）a=1，
a2+2a-1=0，
解得a=-1±
∵a＞0，
∴a=
-1，∴P2（
+1，-1）．故答案为：（
+1，-1）．点评：此题主要考查了反比例函数比例系数k的意义的应用；判断出所求坐标的横纵坐标的代数式是解决本题的关键．
练习册系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
如图，P1、P2、P3是双曲线上的三点．过这三点分别作y轴的垂线，得到三个三角形P1A10，P2A20，P3A30，设它们的面积分别是S1、S2、S3，则（ ）| A、S1＜S2＜S3 | B、S2＜S1＜S3 | C、S1＜S3＜S2 | D、S1=S2=S3 |
如图，P1，P2，P3是双曲线上的三点，过这三点分别作y的垂线，得到三个△P1A1O，△P2A2O，△P3A3O，设它们的轴面积分别为S1，S2，S3，则S1，S2，S3的大小关系是（ ）| A、S1=S2=S3 | B、S1=S3＜S2 | C、S2＞S3＞S1 | D、无法确定 |
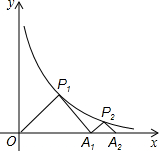（2011•峨眉山市二模）如图，P1、P2是函数
（x＞0）上的点，若△P1OA1、△P2A1A2是等腰直角三角形，斜边OA1、A1A2都在x轴上，则点P2的坐标是 ．