题目内容
（2006•绵阳）（1）解不等式组：
；（2）化简：（
-
）÷
．
【答案】分析：先解不等式组中的每一个不等式，再求出两不等式的公共部分；化简时要注意通分时一定要细心．
解答：解：（1）
，
将①整理得：-2x＞-2．
解得：x＜1．
将②整理为：-
≥
，
解得：x≤-
．
∴原不等式组的解集为x≤-
．
（2）解：原式=
•
=
•
=
•
=-
．
点评：本题考查综合运算能力，是各地中考题中常见的计算题型．分式运算能因式分解的要先因式分解．
解答：解：（1）
，将①整理得：-2x＞-2．
解得：x＜1．
将②整理为：-
≥，解得：x≤-
．∴原不等式组的解集为x≤-
．（2）解：原式=
•=
•=
•=-
．点评：本题考查综合运算能力，是各地中考题中常见的计算题型．分式运算能因式分解的要先因式分解．
练习册系列答案
相关题目
（2006•绵阳）某产品每件的成本是120元，为了解市场规律，试销阶段按两种方法进行销售，结果如下：
方案甲：保持每件150元的售价不变，此时日销售量为50件；
方案乙：不断地调整售价，此时发现日销售量y（件）是售价x（元）的一次函数，且前三天的销售情况如下表：
（1）如果方案乙中的第四天、第五天售价均为180元，那么前五天中，哪种方案的销售总利润大？
（2）分析两种方案，为获得最大日销售利润，每件产品的售价应写为多少元此时，最大日销售利润S是多少？（注：销售利润=销售额-成本额，销售额=售价×销售量）．
方案甲：保持每件150元的售价不变，此时日销售量为50件；
| x （元） | 130 | 150 | 160 |
| y （件） | 70 | 50 | 40 |
（1）如果方案乙中的第四天、第五天售价均为180元，那么前五天中，哪种方案的销售总利润大？
（2）分析两种方案，为获得最大日销售利润，每件产品的售价应写为多少元此时，最大日销售利润S是多少？（注：销售利润=销售额-成本额，销售额=售价×销售量）．
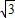
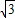-1
+1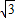
-1
+1