题目内容
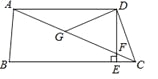
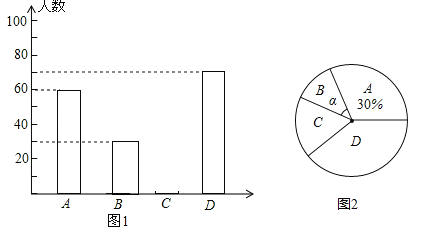
【题目】如图，E为ABCD中DC边的延长线上的一点，且CE=DC，连接AE交BC于点F，连接AC、BE．
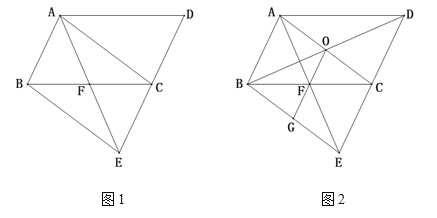
（1）如图1，求证：AF=EF；
（2）连接BD交AC于点O，连接OF并延长交BE于点G，直接写出图中所有长度是OF二倍的线段．
【答案】（1）证明见解析 （2）
，证明见解析
【解析】
（1）根据平行四边形的性质以及对顶角相等可证明
，即可得证
；
（2）根据平行四边形的性质可证明
，即可得证
，再根据平行四边形的性质可得
，即可求解．
（1）∵四边形ABCD是平行四边形
∴
∴
，
∵
∴
在△ABF和△ECF中
∴
∴；
（2）
∵，
∴四边形ABEC是平行四边形，
∴
，
∴
在△AOF和△EGF中
∴
∴
∴
∵四边形ABCD是平行四边形
∴
∴
∵
∴四边形OCEG是平行四边形
∴
∴
故图中所有长度是OF二倍的线段有．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
