题目内容
(2007•镇江)在直角坐标系中有两条直线l1、l2,直线l1所对应的函数关系式为y=x-2,如果将坐标纸折叠,使l1与l2重合,此时点(-1,0)与点(0,-1)也重合,则直线l2所对应的函数关系式为( )A.y=x-2
B.y=x+2
C.y=-x-2
D.y=-x+2
【答案】分析:因为本题中将坐标纸折叠,使l1与l2重合,此时点(-1,0)与点(0,-1)也重合,可知是沿直线y=x折叠,而直线l1与直线y=x平行;
折叠后l1与l2重合,则l2也与直线y=x平行,从而可设直线l2所对应的函数关系式为y=x+k,而y=x-2过点(0,-2),该点折叠后的对应点为(-2,0),进而可利用方程求解.
解答:解:∵将坐标纸折叠,使l1与l2重合,此时点(-1,0)与点(0,-1)也重合,
∴是沿直线y=x折叠,
∵直线l1与直线y=x平行,折叠后l1与l2重合,则l2也与直线y=x平行,
∴设直线l2的函数关系式为y=x+k,
∵y=x-2过点(0,-2),该点折叠后的对应点为(-2,0),
∴直线l2过点(-2,0),
∴0=-2+k,
∴k=2即直线l2所对应的函数关系式为:y=x+2.
故选B.
点评:此类题目需分析折叠的特点,建立直线间的联系,然后将点的坐标代入解析式,利用方程解决问题.
折叠后l1与l2重合,则l2也与直线y=x平行,从而可设直线l2所对应的函数关系式为y=x+k,而y=x-2过点(0,-2),该点折叠后的对应点为(-2,0),进而可利用方程求解.
解答:解:∵将坐标纸折叠,使l1与l2重合,此时点(-1,0)与点(0,-1)也重合,
∴是沿直线y=x折叠,
∵直线l1与直线y=x平行,折叠后l1与l2重合,则l2也与直线y=x平行,
∴设直线l2的函数关系式为y=x+k,
∵y=x-2过点(0,-2),该点折叠后的对应点为(-2,0),
∴直线l2过点(-2,0),
∴0=-2+k,
∴k=2即直线l2所对应的函数关系式为:y=x+2.
故选B.
点评:此类题目需分析折叠的特点,建立直线间的联系,然后将点的坐标代入解析式,利用方程解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(2007•镇江)探索、研究:下图是按照一定的规律画出的一列“树型”图,下表的n表示“树型”图的序号,an表示第n个“树型”图中“树枝”的个数.
图: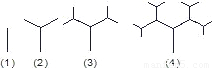
表:
(1)根据“图”、“表”可以归纳出an关于n的关系式为______.
若直线l1经过点(a1,a2)、(a2,a3),求直线l1对应的函数关系式,并说明对任意的正整数n,点(an,an+1)都在直线l1上.
(2)设直线l2:y=-x+4与x轴相交于点A,与直线l1相交于点M,双曲线y=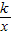 (x>0)经过点M,且与直线l2相交于另一点N.
(x>0)经过点M,且与直线l2相交于另一点N.
①求点N的坐标,并在如图所示的直角坐标系中画出双曲线及直线l1、l2.
②设H为双曲线在点M、N之间的部分(不包括点M、N),P为H上一个动点,点P的横坐标为t,直线MP与x轴相交于点Q,当t为何值时,△MQA的面积等于△PMA的面积的2倍又是否存在t的值,使得△PMA的面积等于1?若存在,求出t的值;若不存在,请说明理由.
③在y轴上是否存在点G,使得△GMN的周长最小?若存在,求出点G的坐标;若不存在,请说明理由.
图:

表:
| n | 1 | 2 | 3 | 4 | … |
| an | 1 | 3 | 7 | 15 | … |
若直线l1经过点(a1,a2)、(a2,a3),求直线l1对应的函数关系式,并说明对任意的正整数n,点(an,an+1)都在直线l1上.
(2)设直线l2:y=-x+4与x轴相交于点A,与直线l1相交于点M,双曲线y=
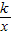 (x>0)经过点M,且与直线l2相交于另一点N.
(x>0)经过点M,且与直线l2相交于另一点N.①求点N的坐标,并在如图所示的直角坐标系中画出双曲线及直线l1、l2.
②设H为双曲线在点M、N之间的部分(不包括点M、N),P为H上一个动点,点P的横坐标为t,直线MP与x轴相交于点Q,当t为何值时,△MQA的面积等于△PMA的面积的2倍又是否存在t的值,使得△PMA的面积等于1?若存在,求出t的值;若不存在,请说明理由.
③在y轴上是否存在点G,使得△GMN的周长最小?若存在,求出点G的坐标;若不存在,请说明理由.


