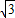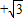题目内容
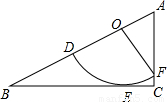
 如图所示为扇形DOF与直角△ABC的重迭情形,其中O,D,F分别在AB,OB,AC上,且
如图所示为扇形DOF与直角△ABC的重迭情形,其中O,D,F分别在AB,OB,AC上,且 与BC相切于E点.若OF=3,∠DOF=∠ACB=90°,且
与BC相切于E点.若OF=3,∠DOF=∠ACB=90°,且 :
: =2:1,则AB的长度为
=2:1,则AB的长度为
- A.6
- B.3

- C.6

- D.
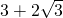
C
分析:连接OE,由切线的性质知:OE⊥BC,由弧DE、弧EF的比例关系,可得∠DOE、∠EOF的度数,即可得∠AFO的度数;在Rt△BOE和Rt△AOF中,可根据⊙O的半径求得BO、OA的长,相加即可.
解答: 解:连接OE,则OE⊥BC;
解:连接OE,则OE⊥BC;
∵ :
: =2:1,且∠DOF=90°,
=2:1,且∠DOF=90°,
∴∠DOE=60°,∠EOF=30°;
在Rt△BOE中,OE=OF=3,∠BOE=60°,则OB=6,
在Rt△AOF中,OF=3,∠AFO=∠EOF=30°,则OA= ,
,
∴AB=OB+OA=6+ ,故选C.
,故选C.
点评:此题主要考查了切线的性质以及圆心角、弧的关系,难度不大.
分析:连接OE,由切线的性质知:OE⊥BC,由弧DE、弧EF的比例关系,可得∠DOE、∠EOF的度数,即可得∠AFO的度数;在Rt△BOE和Rt△AOF中,可根据⊙O的半径求得BO、OA的长,相加即可.
解答:
 解:连接OE,则OE⊥BC;
解:连接OE,则OE⊥BC;∵
 :
: =2:1,且∠DOF=90°,
=2:1,且∠DOF=90°,∴∠DOE=60°,∠EOF=30°;
在Rt△BOE中,OE=OF=3,∠BOE=60°,则OB=6,
在Rt△AOF中,OF=3,∠AFO=∠EOF=30°,则OA=
 ,
,∴AB=OB+OA=6+
 ,故选C.
,故选C.点评:此题主要考查了切线的性质以及圆心角、弧的关系,难度不大.

练习册系列答案
相关题目
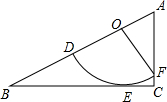 如图所示为扇形DOF与直角△ABC的重迭情形,其中O,D,F分别在AB,OB,AC上,且
如图所示为扇形DOF与直角△ABC的重迭情形,其中O,D,F分别在AB,OB,AC上,且
 与BC相切于E点.若OF=3,∠DOF=∠ACB=90°,且
与BC相切于E点.若OF=3,∠DOF=∠ACB=90°,且 :
: =2:1,则AB的长度为( )
=2:1,则AB的长度为( )



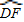 与BC相切于E点.若OF=3,∠DOF=∠ACB=90°,且
与BC相切于E点.若OF=3,∠DOF=∠ACB=90°,且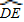 :
: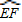 =2:1,则AB的长度为( )
=2:1,则AB的长度为( )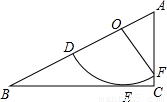
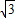
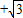
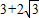
 与BC相切于E点.若OF=3,∠DOF=∠ACB=90°,且
与BC相切于E点.若OF=3,∠DOF=∠ACB=90°,且 :
: =2:1,则AB的长度为( )
=2:1,则AB的长度为( )

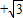

 与BC相切于E点.若OF=3,∠DOF=∠ACB=90°,且
与BC相切于E点.若OF=3,∠DOF=∠ACB=90°,且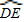 :
: =2:1,则AB的长度为( )
=2:1,则AB的长度为( )