题目内容
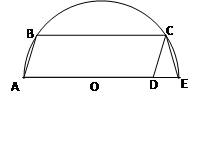
如图，在半径为
，圆心角等于45°的扇形
内部作一个正方形
，使点
在
上，点
在
上，点
在
上，则阴影部分的面积为（结果保留
） ．
，圆心角等于45°的扇形内部作一个正方形，使点在上，点在上，点在上，则阴影部分的面积为（结果保留） ．
首先要明确S阴影=S扇形OAB-S△OCD-S正方形CDEF，然后依面积公式计算即可．
解：连接OF，
∵∠AOD=45°，四边形CDEF是正方形，
∴OD=CD=DE=EF，
于是Rt△OFE中，OE=2EF，
∵OF=
，EF2+OE2=OF2，
∴EF2+（2EF）2=5，
解得：EF=1，
∴EF=OD=CD=1，
∴S阴影=S扇形OAB-S△OCD-S正方形CDEF=
×1×1-1×1=．
解：连接OF，∵∠AOD=45°，四边形CDEF是正方形，
∴OD=CD=DE=EF，
于是Rt△OFE中，OE=2EF，
∵OF=
，EF2+OE2=OF2，∴EF2+（2EF）2=5，
解得：EF=1，
∴EF=OD=CD=1，
∴S阴影=S扇形OAB-S△OCD-S正方形CDEF=
×1×1-1×1=．
练习册系列答案
相关题目
