Question

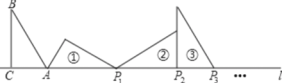
【题目】如图，Rt△ABC中，∠ACB=90°，AC=1，∠B=30°，且AC边在直线l上，将△ABC绕点A顺时针旋转到位置①可得到点P1，此时；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时；……，按此规律继续旋转，直至得到点为止，则=___________．

Answer 1

【答案】2012+671．

【解析】

仔细审题，发现将Rt△ABC绕A顺时针旋转，每旋转一次，AP的长度依次增加2，，1，且三次一循环，按此规律即可求解．

解：如图所示，

∵Rt△ABC中，∠ACB=90°，∠B=30°，AC=1，

∴AB=2，BC=，

∵由旋转的性质可知：△ABC≌△AP1E

∴AB=AP1=2，

∵△ABC≌FP1P2，

∴P1P2=BC，

∴AP2=2+，

同理可的：AP3=3+，

∵2012÷3=670…2，

∴AP2012=670×(3+)+2+=2012+671．

故答案为：2012+671．