题目内容
18.反比例函数y=$\frac{2a-1}{x}$的图象有一支位于第一象限,则常数a的取值范围是a$>\frac{1}{2}$.分析 根据反比例函数的性质:当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小可得2a-1>0,再解不等式即可.
解答 解:∵反比例函数y=$\frac{2a-1}{x}$的图象有一支位于第一象限,
∴2a-1>0,
解得:a>$\frac{1}{2}$.
故答案为:a$>\frac{1}{2}$.
点评 此题主要考查了反比例函数的性质,关键是掌握反比例函数$y=\frac{k}{x}$(k≠0),(1)k>0,反比例函数图象在一、三象限;(2)k<0,反比例函数图象在第二、四象限内.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
9.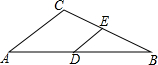 如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )
如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )
 如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )
如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
13.国家统计局数据显示,截至2014年末全国商品房待售面积约为62200万平方米,该数据用科学记数法可表示为( )
| A. | 6.22×104 | B. | 6.22×107 | C. | 6.22×108 | D. | 6.22×109 |
3.下列运算结果,错误的是( )
| A. | -(-$\frac{1}{2}$)=$\frac{1}{2}$ | B. | (-1)0=1 | C. | (-1)+(-3)=4 | D. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ |
10.计算:3-2×(-1)=( )
| A. | 5 | B. | 1 | C. | -1 | D. | 6 |
7.在排球训练中,甲、乙、丙三人相互传球,由甲开始发球(记作为第一次传球),则经过三次传球后,球仍回到甲手中的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |