题目内容
已知：如图，O为坐标原点，四边形OABC为矩形，A(10，0)，C(0，4)，点D是OA的中点，点P在BC上以每秒1个单位的速度由C向B运动。
（1） 求梯形ODPC的面积S与时间t的函数关系式。
（2）t为何值时，四边形PODB是平行四边形？
（3） 在线段PB上是否存在一点Q，使得ODQP为菱形。若存在求t值，若不存在，说明理由。
（4） 当△OPD为等腰三角形时，求点P的坐标。
（1） 求梯形ODPC的面积S与时间t的函数关系式。
（2）t为何值时，四边形PODB是平行四边形？
（3） 在线段PB上是否存在一点Q，使得ODQP为菱形。若存在求t值，若不存在，说明理由。
（4） 当△OPD为等腰三角形时，求点P的坐标。
解：（1）s=2t+10；
（2）t=5 ；
（3）t=3；
（4） P1(3，4) ， P2(2，4) ， P3(2.5，4) ， P4(8，4)
（2）t=5 ；
（3）t=3；
（4） P1(3，4) ， P2(2，4) ， P3(2.5，4) ， P4(8，4)
练习册系列答案
阅读快车系列答案
相关题目
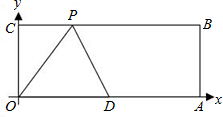
已知：如图，O为坐标原点，四边形OABC为矩形，A（10，0），C（0，4），点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，则P点的坐标为（ ）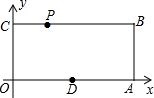
已知，如图，O为坐标原点，四边形OABC为矩形，A（10，0），C（0，4），点D是OA的中点，点P在边BC上以每秒1个单位长的速度由点C向点B运动．
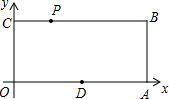已知：如图，O为坐标原点，四边形OABC为矩形，A（10，0），C（0，4），点D是OA的中点，点P在BC上以每秒1个单位的速度由C向B运动．