题目内容
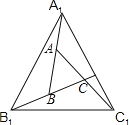
【题目】如图1，在Rt△ABC中，∠B=90°，BC=2AB=8，点D，E分别是边BC，AC的中点，连接DE. 将△EDC绕点C按顺时针方向旋转，记旋转角为α.
（1）问题发现
① 当
时，
；
② 当
时，
（2）拓展探究
试判断：当0°＜α＜360°时，
的大小有无变化？请仅就图2的情况给出证明.
（3）问题解决
当△EDC旋转至A、D、E三点共线时，直接写出线段BD的长.
【答案】（1） 
．．（2） ．（3） 
或
．
【解析】
试题分析：（1）①当α=0°时，在Rt△ABC中，由勾股定理，求出AC的值是多少；然后根据点D、E分别是边BC、AC的中点，分别求出AE、BD的大小，即可求出
的值是多少．
②α=180°时，可得AB∥DE，然后根据
，求出的值是多少即可．
（2）首先判断出∠ECA=∠DCB，再根据
，判断出△ECA∽△DCB，即可求出的值是多少，进而判断出的大小没有变化即可．
（3）根据题意，分两种情况：①点A，D，E所在的直线和BC平行时；②点A，D，E所在的直线和BC相交时；然后分类讨论，求出线段BD的长各是多少即可．
试题解析：（1）①当α=0°时，
∵Rt△ABC中，∠B=90°，
∴AC=
，
∵点D、E分别是边BC、AC的中点，
∴AE=
÷2=
，BD=8÷2=4，
∴
．
②如图1，
，
当α=180°时，
可得AB∥DE，
∵
，
∴
=
．
（2）如图2，
，
当0°≤α＜360°时，
的大小没有变化，
∵∠ECD=∠ACB，
∴∠ECA=∠DCB，
又∵
=
，
∴△ECA∽△DCB，
∴
．
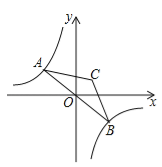
（3）①如图3，
，
∵AC=
，CD=4，CD⊥AD，
∴AD=
，
∵AD=BC，AB=DC，∠B=90°，
∴四边形ABCD是矩形，
∴BD=AC=．
②如图4，连接BD，过点D作AC的垂线交AC于点Q，过点B作AC的垂线交AC于点P，
，
∵AC=，CD=4，CD⊥AD，
∴AD=，
∵点D、E分别是边BC、AC的中点，
∴DE=
AB=×（8÷2）=×4=2，
∴AE=AD-DE=8-2=6，
由（2），可得
，
∴BD=
．
综上所述，BD的长为或．
