Question

【题目】在下列解题过程的空白处填上适当的推理理由或数学表达式：

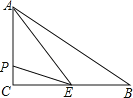
如图，在△ABC中，已知∠ADE＝∠B，∠1＝∠2，FG⊥AB于点G．

求证：CD⊥AB.

证明:∵∠ADE＝∠B（已知），

∴DE∥BC（ ① ），

∵ DE∥BC（已证），

∴ ② （ ③ ），

又∵∠1＝∠2（已知），

∴ ④ （ ⑤ ），

∴CD∥FG（同位角相等，两直线平行），

∴∠CDB＝∠FGB（两直线平行，同位角相等），

∵ FG⊥AB（已知），

∴∠FGB＝90°（垂直的定义）.

∴∠CDB＝90°

∴CD⊥AB（垂直的定义）.

Answer 1

【答案】①同位角相等，两直线平行；②∠1＝∠DCB； ③两直线平行，内错角相等；④∠DCB＝∠2 ；⑤等量代换．

【解析】

根据平行线的判定和性质解答即可．

∵∠ADE＝∠B（已知），

∴DE∥BC（ 同位角相等，两直线平行），

∵ DE∥BC（已证），

∴∠1＝∠DCB （ 两直线平行，内错角相等），

又∵∠1＝∠2（已知），

∴∠DCB＝∠2（等量代换），

∴CD∥FG（同位角相等，两直线平行），

∴∠CDB＝∠FGB（两直线平行，同位角相等），

∵ FG⊥AB（已知），

∴∠FGB＝90°（垂直的定义）．

∴∠CDB＝90°

∴CD⊥AB（垂直的定义）．

故答案为：①同位角相等，两直线平行；②∠1＝∠DCB； ③两直线平行，内错角相等；④∠DCB＝∠2 ；⑤等量代换．