Question

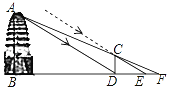
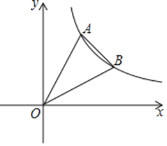
【题目】如图，某测量小组为了测量山BC的高度，在地面A处测得山顶B的仰角45°，然后沿着坡度为1：的坡面AD走了200米到D处，此时在D处测得山顶B的仰角为60°，则山高BC＝_____米（结果保留根号）．

Answer 1

【答案】300+100

【解析】

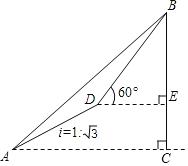
作DF⊥AC于F．解直角三角形分别求出BE、EC即可解决问题.

作DF⊥AC于F．

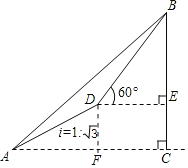
∵DF：AF＝1：，AD＝200米，

∴tan∠DAF＝，

∴∠DAF＝30°，

∴DF＝AD＝×200＝100（米），

∵∠DEC＝∠BCA＝∠DFC＝90°，

∴四边形DECF是矩形，

∴EC＝DF＝100（米），

∵∠BAC＝45°，BC⊥AC，

∴∠ABC＝45°，

∵∠BDE＝60°，DE⊥BC，

∴∠DBE＝90°﹣∠BDE＝90°﹣60°＝30°，

∴∠ABD＝∠ABC﹣∠DBE＝45°﹣30°＝15°，∠BAD＝∠BAC﹣∠DAC＝45°﹣30°＝15°，

∴∠ABD＝∠BAD，

∴AD＝BD＝200（米），

在Rt△BDE中，sin∠BDE＝，

∴BE＝BDsin∠BDE＝200×＝300（米），

∴BC＝BE+EC＝300+100（米）；

故答案为：300+100．