题目内容
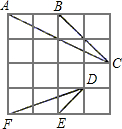 如图所示,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
如图所示,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
填空:∠ABC=________°,BC=________.
135 2
分析:先在Rt△BCG中根据等腰直角三角形的性质求出∠GBC的度数,再根据∠ABC=∠GBC+∠ABG即可得出∠ABC的度数;在Rt△BCH中利用勾股定理即可求出BC的长.
解答: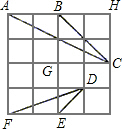 解:∵△BCG是等腰直角三角形,
解:∵△BCG是等腰直角三角形,
∴∠GBC=45°,
∵∠ABG=90°,
∴∠ABC=∠GBC+∠ABG=90°+45°=135°;
∵在Rt△BHC中,BH=2,CH=2,
∴BC=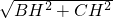 =
= =2
=2 .
.
故答案为:135°;2 .
.
点评:本题考查的是勾股定理,根据题意找出所求的角及边所在的直角三角形,根据勾股定理及直角三角形的性质解答是解答此题的关键.

分析:先在Rt△BCG中根据等腰直角三角形的性质求出∠GBC的度数,再根据∠ABC=∠GBC+∠ABG即可得出∠ABC的度数;在Rt△BCH中利用勾股定理即可求出BC的长.
解答:
 解:∵△BCG是等腰直角三角形,
解:∵△BCG是等腰直角三角形,∴∠GBC=45°,
∵∠ABG=90°,
∴∠ABC=∠GBC+∠ABG=90°+45°=135°;
∵在Rt△BHC中,BH=2,CH=2,
∴BC=
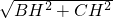 =
= =2
=2 .
.故答案为:135°;2
 .
.点评:本题考查的是勾股定理,根据题意找出所求的角及边所在的直角三角形,根据勾股定理及直角三角形的性质解答是解答此题的关键.

练习册系列答案
相关题目
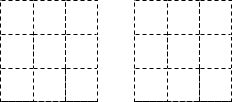
 如图所示,在4×4的方格中每个小正方形的边长是单位1,小正方形的顶点称为格点.现有格点A、B,在方格中任意找一个格点C,则以A、B、C三点为顶点能构成等腰三角形的概率是
如图所示,在4×4的方格中每个小正方形的边长是单位1,小正方形的顶点称为格点.现有格点A、B,在方格中任意找一个格点C,则以A、B、C三点为顶点能构成等腰三角形的概率是 如图所示,在5×5的方格纸上建立直角坐标系,A(1,0),B(0,2),试以5×5的格点为顶点作△ABC与△OAB相似(相似比不为1),并写出C点的坐标.
如图所示,在5×5的方格纸上建立直角坐标系,A(1,0),B(0,2),试以5×5的格点为顶点作△ABC与△OAB相似(相似比不为1),并写出C点的坐标. 如图所示,在一圆柱体的下底边沿A处,不走直线而绕着圆柱侧面,沿一条螺旋形路线绕到B处的最短路线是什么?
如图所示,在一圆柱体的下底边沿A处,不走直线而绕着圆柱侧面,沿一条螺旋形路线绕到B处的最短路线是什么? 如图所示,在3×3的方格内,填写了一些式子和数,图中各行、各列及对角线上三个数之和都相等,请你求出x、y、z的值.
如图所示,在3×3的方格内,填写了一些式子和数,图中各行、各列及对角线上三个数之和都相等,请你求出x、y、z的值.