题目内容
已知O为直线AF上一点,射线OC与射线OB在直线AF同侧且不重合,且OD平分∠AOC,
(1)如图,若∠AOB=86°,∠AOC=30°,求∠DOB和∠DOF的度数;
(2)若射线OE在∠BOC内部,∠AOB=β(其中0°<β<180°),∠DOE=
,请画出草图,结合图形猜想射线OE是图中哪个已知角的平分线?请说明理由.

(1)如图,若∠AOB=86°,∠AOC=30°,求∠DOB和∠DOF的度数;
(2)若射线OE在∠BOC内部,∠AOB=β(其中0°<β<180°),∠DOE=
| β | 2 |

分析:(1)先根据角平分线的定义求出∠AOD的度数,再∠AOB-∠AOD即可求出∠DOB的度数,用180°-∠AOD即可求出∠DOF的度数;
(2)先由已知条件证明出∠DOC+∠COE=∠A0D+∠BOE,再根据角平分线的定义得出∠DOC=∠A0D,由等式的性质即可得出射线OE是∠BOC的平分线.
(2)先由已知条件证明出∠DOC+∠COE=∠A0D+∠BOE,再根据角平分线的定义得出∠DOC=∠A0D,由等式的性质即可得出射线OE是∠BOC的平分线.
解答:解:(1)∵OD平分∠AOC,∠AOC=30°,
∴∠AOD=
∠AOC=15°,
∴∠DOB=∠AOB-∠AOD=86°-15°=71°,
∠DOF=180°-∠AOD=180°-15°=165°;
(2)如图,射线OE是∠BOC的平分线.理由如下:
∵∠AOB=β,∠DOE=
,
∴∠A0D+∠BOE=∠AOB-∠DOE=
,
∴∠DOE=∠A0D+∠BOE,
∴∠DOC+∠COE=∠A0D+∠BOE,
又∵OD平分∠AOC,∴∠DOC=∠A0D,
∴∠COE=∠BOE,即射线OE是∠BOC的平分线.
∴∠AOD=
| 1 |
| 2 |
∴∠DOB=∠AOB-∠AOD=86°-15°=71°,
∠DOF=180°-∠AOD=180°-15°=165°;
(2)如图,射线OE是∠BOC的平分线.理由如下:

∵∠AOB=β,∠DOE=
| β |
| 2 |
∴∠A0D+∠BOE=∠AOB-∠DOE=
| β |
| 2 |
∴∠DOE=∠A0D+∠BOE,
∴∠DOC+∠COE=∠A0D+∠BOE,
又∵OD平分∠AOC,∴∠DOC=∠A0D,
∴∠COE=∠BOE,即射线OE是∠BOC的平分线.
点评:本题考查了角平分线的定义、平角的定义及角的计算,难度中等.(1)中根据角平分线的定义求出∠AOD的度数是解题的关键,(2)中由已知条件证明出∠DOC+∠COE=∠A0D+∠BOE是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


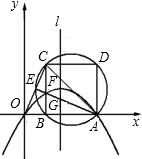 ?若存在,请求出所有这样的点;若不存在,请说明理由.
?若存在,请求出所有这样的点;若不存在,请说明理由.