题目内容
在平面直角坐标系中,抛物线 的顶点是点P,对称轴与x轴相交于点Q,以点P为圆心,PQ长为半径画⊙P,那么下列判断正确的是( )
的顶点是点P,对称轴与x轴相交于点Q,以点P为圆心,PQ长为半径画⊙P,那么下列判断正确的是( )
| A.x轴与⊙P相离; | B.x轴与⊙P相切; |
| C.y轴与⊙P与相切; | D.y轴与⊙P相交. |
B.
解析试题分析:根据抛物线解析式写出顶点P和点Q的坐标,然后求出PQ的长,再根据直线与圆的位置关系解答.
由题意得,顶点P(2,1),Q(2,0),
所以PQ=1,
即⊙P的半径为1,
∵点P到x轴的距离为1,到y轴的距离为2,
∴x轴与⊙P相切,y轴与⊙P相离.
故选B.
考点:二次函数综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将函数 变形为
变形为 的形式,正确的是( )
的形式,正确的是( )
A. | B. |
C. | D. |
已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a-b+c<0;则正确的结论是( )
| A.①②③④ | B.②④⑤ | C.②③④ | D.①④⑤ |
根据下列表格中二次函数y=ax2+bx+c的自变量 与函数值
与函数值 的对应值,判断方程ax2+b x+c=0(a≠0)的一个解
的对应值,判断方程ax2+b x+c=0(a≠0)的一个解 的范围是( )
的范围是( )
 | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | -0.03 | -0.01 | 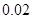 |  |
C.6.18<x<6.19 D.6.19<x<6.20
把抛物线 向左平移3个单位,再向下平移2个单位后,所得的抛物线的表达式是
向左平移3个单位,再向下平移2个单位后,所得的抛物线的表达式是
A. | B. |
C. | D. |
当a<0时,抛物线y=x2+2ax+1+2a2的顶点在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
二次函数 的图象与
的图象与 轴交点的横坐标是( )
轴交点的横坐标是( )
A. 和 和 | B. 和 和 | C. 和 和 | D. 和 和 |
已知二次函数y=a(x+1)2-b(a≠0)有最小值,则a,b的大小关系为 ( )
| A.a>b | B.a<b |
| C.a=b | D.不能确定 |
 Rt
Rt (
( )的直角边与正方形
)的直角边与正方形 的边长均为2,且
的边长均为2,且 与
与 在同一直线上,开始时点
在同一直线上,开始时点 与点
与点 重合,让
重合,让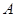 与点
与点 重合为止.设
重合为止.设 的长为
的长为 ,
, ,则
,则
