题目内容
在△ABC中,∠BAC=90°,AB=AC=2
.
(1)如图1,若以点A为圆心、r为半径的⊙A与BC相切于点D,求r.
(2)如图2,若⊙A的半径r=1,点O在BC上运动(点O与B、C不重合),设BO=x,△AOC的面积为y.①求y关于x的函数关系式,并写出x的取值范围.
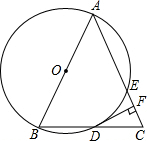
②如图2,以点O为圆心,BO长为半径作圆,当⊙O与⊙A相切时,求△AOC的面积.

| 2 |
(1)如图1,若以点A为圆心、r为半径的⊙A与BC相切于点D,求r.
(2)如图2,若⊙A的半径r=1,点O在BC上运动(点O与B、C不重合),设BO=x,△AOC的面积为y.①求y关于x的函数关系式,并写出x的取值范围.
②如图2,以点O为圆心,BO长为半径作圆,当⊙O与⊙A相切时,求△AOC的面积.

(1)∵△ABC中,∠BAC=90°,AB=AC=2
,
∴△ABC为等腰直角三角形,
∴BC=4,
∵⊙A与BC相切于点D,
∴AD=r,AD⊥BC,
∴AD为BC边上的中线,
∴r=AD=
BC=2,
(2)①作AD⊥BC于点D,
∵△ABC为等腰直角三角形,BC=4,
∴AD为BC边上的中线,
∴AD=
BC=2,
∴S△AOC=
OC•AD,
∵BO=x,△AOC的面积为y,
∴y=4-x(0<x<4),
②过O点作OE⊥AB交AB于E,
∵⊙A的半径为1,OB=x,
当两圆外切时,
∴OA=1+x,
∵△ABC为等腰直角三角形,
∴∠B=45°,
∴BE=OE=
x,
∴在△AEO中,AO2=AE2+OE2=(AB-BE)2+OE2,
∴(1+x)2=(2
-
x)2+(
x)2,
∴x=
,
∵△AOC面积=y=4-x,
∴△AOC面积=
;
当两圆内切时,
∴OA=x-1,
∵AO2=AE2+OE2=(AB-BE)2+OE2,
∴(x-1)2=(2
-
x)2+(
x)2,
∴x=
,
∴△AOC面积=y=4-x=4-
=
,
∴△AOC面积为
或
.
| 2 |
∴△ABC为等腰直角三角形,
∴BC=4,
∵⊙A与BC相切于点D,
∴AD=r,AD⊥BC,
∴AD为BC边上的中线,
∴r=AD=
| 1 |
| 2 |
(2)①作AD⊥BC于点D,

∵△ABC为等腰直角三角形,BC=4,
∴AD为BC边上的中线,
∴AD=
| 1 |
| 2 |
∴S△AOC=
| 1 |
| 2 |
∵BO=x,△AOC的面积为y,
∴y=4-x(0<x<4),
②过O点作OE⊥AB交AB于E,

∵⊙A的半径为1,OB=x,
当两圆外切时,
∴OA=1+x,
∵△ABC为等腰直角三角形,
∴∠B=45°,
∴BE=OE=
| ||
| 2 |
∴在△AEO中,AO2=AE2+OE2=(AB-BE)2+OE2,
∴(1+x)2=(2
| 2 |
| ||
| 2 |
| ||
| 2 |

∴x=
| 7 |
| 6 |
∵△AOC面积=y=4-x,
∴△AOC面积=
| 17 |
| 6 |
当两圆内切时,
∴OA=x-1,
∵AO2=AE2+OE2=(AB-BE)2+OE2,
∴(x-1)2=(2
| 2 |
| ||
| 2 |
| ||
| 2 |
∴x=
| 7 |
| 2 |
∴△AOC面积=y=4-x=4-
| 7 |
| 2 |
| 1 |
| 2 |
∴△AOC面积为
| 17 |
| 6 |
| 1 |
| 2 |

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目

 45°.
45°.




