Question

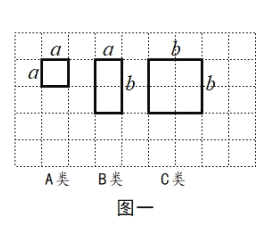
【题目】如图一，现有足够多的边长为的小正方形纸片(类)、长为宽为的长方形纸片(类)以及边长为的大正方形纸片(类)．

　　　　

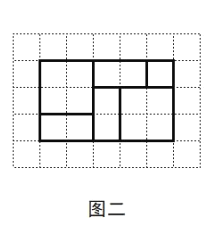
如图二，小明利用上述三种纸片各若干张，拼出了一个长为，宽为的长方形，并用这个长方形解释了等式是成立的．

（1）若取图一中的纸片若干张(三种都要取到)拼成一个长方形(所取纸片用完无剩余)，使它的长和宽分别为，请你通过计算说明需要类卡片多少张；

（2）若取类纸片张，类纸片张，类纸片张，能拼成一个长方形吗(所取纸片用完无剩余)？请你在图三中画出示意图并在下面直接写出能用该长方形来解释成立的等式；

　　　

（3）如图四，大正方形的边长为，小正方形的边长为，用四个完全相同的长方形的长和宽为别为．请你通过观察或计算，判断下列个式子是否成立，将其中成立的式子的都填写在横线上： (直接填写序号)．

①；

②；

③；

④．

Answer 1

【答案】（1）需要B类纸片3张；（2）如图所示见解析；；（3）①②④．

【解析】

（1）根据整式的乘法得到，故需要类卡片3张；

（2）根据，故作出长为，宽为的矩形即可求解；

（3）根据正方形的边长相等可得，故可判断①，根据面积的特点得到n2+4xy=m2，再根据完全平方公式和平方差公式的变形即可求解．

（1）

∴需要B类纸片3张；

（2）如图所示

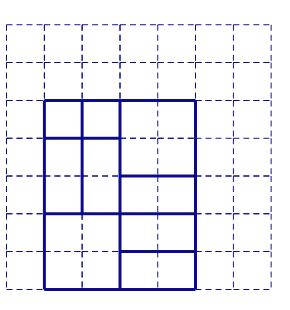
等式为：；

（3）根据图形可得，故①正确；

根据图形面积的特点得到n2+4xy=m2，

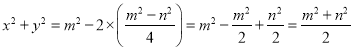∴，②正确；

∵

∴

∴=，④正确；

∵x-y不一定等于2n

∴不一定成立，③错误

故答案为：①②④．