Question

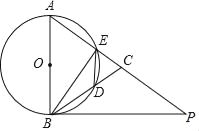
【题目】如图①，在正方形中，点，分别在、上，且．

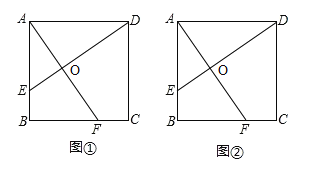
（1）试探索线段、的关系，写出你的结论并说明理由；

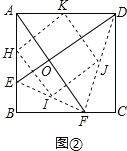
（2）连接、，分别取、、、的中点、、、，四边形是什么特殊平行四边形？请在图②中补全图形，并说明理由．

Answer 1

【答案】（1）AF＝DE，AF⊥DE，理由见详解；（2）四边形HIJK是正方形，补图、理由见详解．

【解析】

（1）根据已知利用SAS判定△DAE≌△ABF，由全等三角形的判定方法可得到AF＝DE，∠BAF＝∠ADE，再由直角三角形的两个锐角互余和有两个角互余的三角形是直角三角形可证得AF⊥DE．

（2）根据已知可得HK，KJ，IJ，HI都是中位线，由全等三角形的判定可得到四边形四边都相等且有一个角是直角，从而来可得到该四边形是正方形．

解：（1）AF＝DE， AF⊥DE．

∵ABCD是正方形，

∴AB＝AD，∠DAB＝∠ABC＝90°，

∵AE＝BF，

∴△DAE≌△ABF，

∴AF＝DE，∠BAF＝∠ADE．

∵∠DAB＝90°，

∴∠BAF+∠DAF＝90°，

∴∠ADE+∠DAF＝90°，

∴AF⊥DE．

∴AF＝DE，AF⊥DE．

（2）四边形HIJK是正方形．

如下图，H、I、J、K分别是AE、EF、FD、DA的中点，

∴HI＝KJ＝AF，HK＝IJ＝ED，

∵AF＝DE，

∴HI＝KJ＝HK＝IJ，

∴四边形HIJK是菱形，

∵△DAE≌△ABF，

∴∠ADE＝∠BAF，

∵∠ADE+∠AED＝90°，

∴∠BAF+∠AED＝90°，

∴∠AOE＝90°

∴∠KHI＝90°，

∴四边形HIJK是正方形．