Question

【题目】如图，AC⊥BC，AC=BC=2，以AC为直径作半圆，圆心为点O；以点C为圆心，BC为半径作⊙C，过点O作BC的平行线交两弧于点D、E，则阴影部分的面积是______．

Answer 1

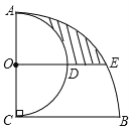
【答案】

【解析】

如图，图中S阴影=S扇形ACB-S扇形AOD-S扇形ECB-S△OCE．根据已知条件易求得OA=OC=OD=2，BC=CE=4．∠ECB=∠OEC=30°，所以由扇形面积公式、三角形面积公式进行解答即可．

如图，连接CE．

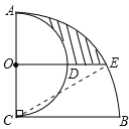
∵AC⊥BC，AC=BC=2，以AC为直径作半圆，圆心为点O；

以点C为圆心，BC为半径作，

∴∠ACB=90°，OA=OC=OD=1，BC=CE=2．

又∵OE∥BC，

∴∠AOE=∠COE=90°．

∴在直角△OEC中，OC=CE，

∴∠OEC=30°，OE=．

∴∠ECB=∠OEC=30°，

∴S阴影=S扇形ACB-S扇形AOD-S扇形ECB-S△OCE

=---×1×

=π-．

故答案为：