题目内容
【题目】已知,两正方形在数轴上运动,起始状态如图所示.A、F表示的数分别为-2、10,大正方形的边长为4个单位长度,小正方形的边长为2个单位长度,两正方形同时出发,相向而行,小正方形的速度是大正方形速度的两倍,两个正方形从相遇到刚好完全离开用时2秒.完成下列问题:
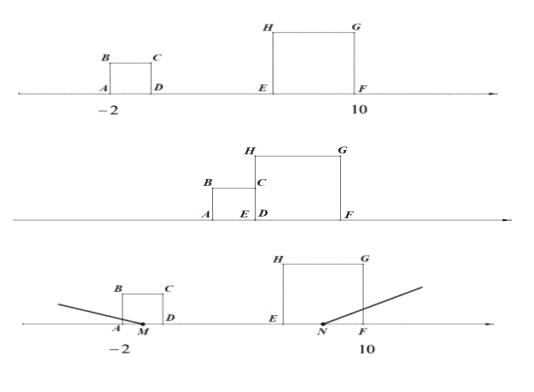
(1)求起始位置D、E表示的数;
(2)求两正方形运动的速度;
(3)M、N分别是AD、EF中点,当正方形开始运动时,射线MA开始以15°/s的速度顺时针旋转至MD结束,射线NF开始以30°/s的速度逆时针旋转至NE结束,若两射线所在直线互相垂直时,求MN的长.
【答案】(1)0,6;(2)小正方形速度2个单位/秒,大正方形速度1个单位/秒;(3)t=2, MN=3,t=6, MN=9
【解析】
(1)利用图象和正方形的边长即可得出;
(2)设小正方形的速度是2x个单位/秒,大正方形的速度是x个单位/秒,然后列方程计算即可;
(3)由题意可得若想要两射线所在直线互相垂直,则有①15°t+30°t=90°或②15°t+30°t=270°
两种情况,根据两种情况分别讨论即可.
(1)∵A、F表示的数分别为-2、10,大正方形的边长为4个单位长度,小正方形的边长为2个单位长度,
∴D表示的数为:-2+2=0,E表示的数为:10-4=6;
(2)解:设小正方形的速度是2x个单位/秒,大正方形的速度是x个单位/秒,
则有2(2x+x)=2+4,
解得:x=1,
∴小正方形的速度是2个单位/秒,
故小正方形速度2个单位/秒,大正方形速度1个单位/秒;
(3)设运动时间为t,
由题意可得若想要两射线所在直线互相垂直,
则有①15°t+30°t=90°或②15°t+30°t=270°,
①15°t+30°t=90°,解得t=2,
此时小正方形运动了4个单位,D点在数字4的位置,大正方形运动了2个单位,E点也在数字4的位置,即D,E重合,
∵M、N分别是AD、EF中点,
∴MN=3;
②15°t+30°t=270°,解得t=6,
此时小正方形运动了12个单位,D点在数字12的位置,大正方形运动了6个单位,E点在数字0的位置,
∵M、N分别是AD、EF中点,
∴此时M点位于数字11的位置,N点位于数字2的位置,
∴MN=11-2=9;