Question

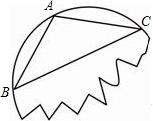如图是一残破圆轮，A、B、C是其弧上三个点．
（1）用尺规作出圆轮的圆心．（保留作图痕迹，不写作法）
（2）设△ABC是等腰三角形，底边BC=10，腰AB=6，求残破圆轮的半径R．（结果保留根号）

Answer 1

分析：（1）分别作出AB和AC的中垂线，两直线的交点即为圆心．
（2）连接OB和OA，根据题意可知OA⊥BC，根据Rt△ABF和Rt△ABO使用两次勾股定理即可得出半径．

解答：解：（1）分别作出AB和AC的中垂线，两直线的交点即为圆心．

（2）连接OB和OA，根据题意可知OA⊥BC，
F为BC的中点，
在Rt△ABF中，AB=6，BF=5，
则AF=

11

，
在Rt△BOF中，BF=5，OF=OB-

11

，
则有OB=

BF2+OF2

= 

BF2+(OB- 11 )2

，
OB²=5²+（OB-

11

）²，
2

11

OB=25+11，
得OB=

18 11

11

；
即残破圆轮的半径为

18 11

11

．

点评：本题考查了如何根据已知的弦作出圆的直径和根据勾股定理解直角三角形．