题目内容
如图,直线OC、BC的函数关系式分别是:y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0< x<3)
x<3)
(1)求点C的坐标,并回答当x取何值时y1>y2?
(2)求△COB的面积;
(3)是否存在点P,使CP将△COB分成的两部分面积之比为1:2?若存在,请求出点P的坐标;若不存在,请说明理由.
 x<3)
x<3)(1)求点C的坐标,并回答当x取何值时y1>y2?
(2)求△COB的面积;
(3)是否存在点P,使CP将△COB分成的两部分面积之比为1:2?若存在,请求出点P的坐标;若不存在,请说明理由.
分析:(1)首先根据直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,列出方程组
,求得两直线的交点坐标.
(2)先作CD⊥x轴于点D,求出D点的坐标,再根据直线y2=-2x+6与x轴交于B点,求出点B的坐标,即可得出S△BOC;
(3)根据CP将△COB分成的两部分面积之比为1:2,分两种情况得出①S△COP=
S△BOC,再求出△COD的面积,得出OP=1,即可得出P点的坐标;②S△COP=
S△BOC,求出△COD的面积,得出OP=2,即可得出P点的坐标;
|
(2)先作CD⊥x轴于点D,求出D点的坐标,再根据直线y2=-2x+6与x轴交于B点,求出点B的坐标,即可得出S△BOC;
(3)根据CP将△COB分成的两部分面积之比为1:2,分两种情况得出①S△COP=
| 1 |
| 3 |
| 2 |
| 3 |
解答: 解:(1)解方程组
解:(1)解方程组
,
解得
,
∴C点坐标为(2,2);
∴当x>2时,y1>y2;
(2)如上图,作CD⊥x轴于点D,则D(2,0),
∵直线y2=-2x+6与x轴交于B点,
∴B(3,0),
∴S△BOC=
OB•CD=
×3×2=3
(3)∵CP将△COB分成的两部分面积之比为1:2,
∴①S△COP=
S△BOC
=
×3=1,
∴
OP•CD=
×OP•2=1,
∴OP=1,
∴P点的坐标(1,0);
②S△COP=
S△BOC
=
×3=2,
∴
OP•CD=
×OP•2=2,
∴OP=2,
∴P点的坐标(2,0);
 解:(1)解方程组
解:(1)解方程组
|
解得
|
∴C点坐标为(2,2);
∴当x>2时,y1>y2;
(2)如上图,作CD⊥x轴于点D,则D(2,0),
∵直线y2=-2x+6与x轴交于B点,
∴B(3,0),
∴S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
(3)∵CP将△COB分成的两部分面积之比为1:2,
∴①S△COP=
| 1 |
| 3 |
=
| 1 |
| 3 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴OP=1,
∴P点的坐标(1,0);
②S△COP=
| 2 |
| 3 |
=
| 2 |
| 3 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴OP=2,
∴P点的坐标(2,0);
点评:此题主要考查平面直角坐标系中图形的面积的求法.解答此题的关键是根据一次函数的特点,分别求出各点的坐标再计算.本题是函数与三角形相结合的问题,在图形中渗透运动的观点是中考中经常出现的问题.

练习册系列答案
相关题目
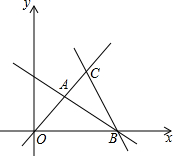 交于点A.
交于点A.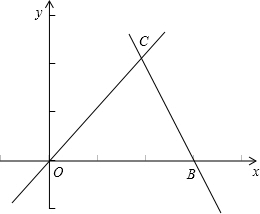 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.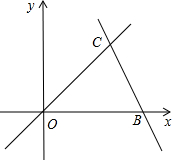 如图,直线OC、BC的函数关系式分别为y=x和y=-2x+6,动点P(x,0)在OB上移动(0<x<3),过点P作直线l与x轴垂直.
如图,直线OC、BC的函数关系式分别为y=x和y=-2x+6,动点P(x,0)在OB上移动(0<x<3),过点P作直线l与x轴垂直.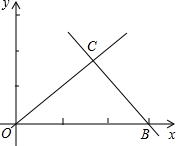 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直. 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6.