题目内容
给定一个正整数n,凸n边形中最多有多少个内角等于150°?并说明理由.
解:设凸n边形最多有k个内角等于150°,则每个150°内角的外角都等于30°,
而凸n边形的n个外角和为360°,所以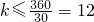 ,
,
只有当n=12时,
k才有最大值12.
下面我们讨论n≠12时的情况:
(1)当n>12时,显然,k的值是11;
(2)当n=3,4,5,6,7时,k的值分别为1,2,3,4,5;
(3)当n=8,9,10,11时,k的值分别为7,8,9,10.
综上所述,当3≤n≤7时,凸n边形最多有n-2个内角等于150°;
当8≤n≤11时,凸n边形最多有n-1个内角等于150°;
当n=12时,凸n边形最多有12个内角等于150°;
当n>12时,凸n边形最多有11个内角等于150°.
分析:设凸n边形最多有k个内角等于150°,则每个150°内角的外角都等于30°,根据凸n边形的n个外角和为360°可计算出k≤12,当n=12时,k有最大值12,再讨论当n>12时,当n=3,4,5,6,7时;当n=8,9,10,11时,k的值.
点评:此题考查了多边形的内角和与外角和的知识.此题难度较大,注意掌握分类讨论思想的应用是解此题的关键.
而凸n边形的n个外角和为360°,所以
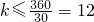 ,
,只有当n=12时,
k才有最大值12.
下面我们讨论n≠12时的情况:
(1)当n>12时,显然,k的值是11;
(2)当n=3,4,5,6,7时,k的值分别为1,2,3,4,5;
(3)当n=8,9,10,11时,k的值分别为7,8,9,10.
综上所述,当3≤n≤7时,凸n边形最多有n-2个内角等于150°;
当8≤n≤11时,凸n边形最多有n-1个内角等于150°;
当n=12时,凸n边形最多有12个内角等于150°;
当n>12时,凸n边形最多有11个内角等于150°.
分析:设凸n边形最多有k个内角等于150°,则每个150°内角的外角都等于30°,根据凸n边形的n个外角和为360°可计算出k≤12,当n=12时,k有最大值12,再讨论当n>12时,当n=3,4,5,6,7时;当n=8,9,10,11时,k的值.
点评:此题考查了多边形的内角和与外角和的知识.此题难度较大,注意掌握分类讨论思想的应用是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(1)填表:
| n(凸多边形的边数) | 3 | 4 | 5 | … |
| m(凸多边形中角度等于135°的内角个数的最大值) | ________ | ________ | ________ | ______ |
(2)猜想给定一个正整数n,凸n边形最多有m个内角等于135°,则m与n之间有怎样的关系?
(3)取n=7验证你的猜想是否成立?如果不成立,请给出凸n边形中最多有多少个内角等于135°?并说明理由.
(1)填表:
(2)猜想给定一个正整数n,凸n边形最多有m个内角等于135°,则m与n之间有怎样的关系?
(3)取n=7验证你的猜想是否成立?如果不成立,请给出凸n边形中最多有多少个内角等于135°?并说明理由.
| n(凸多边形的边数) | 3 | 4 | 5 | … |
| m(凸多边形中角度等于135°的内角个数的最大值) | ______ | ______ | ______ | ______ |
(3)取n=7验证你的猜想是否成立?如果不成立,请给出凸n边形中最多有多少个内角等于135°?并说明理由.