题目内容
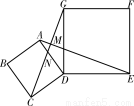
如图,在Rt△OAB中,∠AOB=90°,OA=4,OB=3.⊙O的半径为2,点P是线段AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点.设AP= ,PQ2=
,PQ2= ,则
,则 与
与 的函数图象大致是
的函数图象大致是


A
【解析】
试题分析:过点O作OD⊥AB,则OD= ,∴AD=
,∴AD= ,∴PD=AP-AD=x-
,∴PD=AP-AD=x- ;
;
∴ =
= ,根据垂径定理可得:
,根据垂径定理可得: =
= -4=
-4= ,即y=
,即y= (0≤x≤5)
(0≤x≤5)
考点:二次函数的应用、勾股定理、切线的性质

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 B、
B、 C、
C、 D、
D、
 与一次函数y=2x的图象大致是( ).
与一次函数y=2x的图象大致是( ).
 sin45°-tan60°·cos30°.
sin45°-tan60°·cos30°.
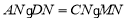
 的顶点坐标是( )
的顶点坐标是( ) ,使它的图象在各自象限内,
,使它的图象在各自象限内, 的值随
的值随 值的增大而减小,这个函数的表达式为 .
值的增大而减小,这个函数的表达式为 .