Question

直角三角形的两锐角的角平分线的夹角中锐角等于（　　）

A．30°

B．36.5°

C．45°

D．60°

Answer 1

分析：根据△ACB为Rt△，利用三角形内角和定理求出∠CAB+∠ABC=90°，再利用角平分线的性质即可求出两锐角的角平分线所夹的锐角的度数．

解答：解：如图所示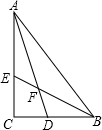
△ACB为Rt△，AD，BE，分别是∠CAB和∠ABC的角平分线，AD，BE相交于一点F．
∵∠ACB=90°，
∴∠CAB+∠ABC=90°
∵AD，BE，分别是∠CAB和∠ABC的角平分线，
∴∠FAB+∠FBA=

1

2

∠CAB+

1

2

∠ABC=45°．
故选C．

点评：本题考查的是三角形内角和定理，根据题意画出图形，利用数形结合求解是解答此题的关键．