题目内容
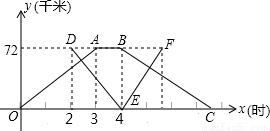
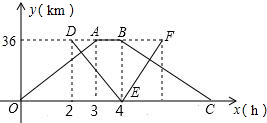 甲、乙两个港口相距36千米,一艘轮船从甲港出发,顺流航行3小时到达乙港.休息1小时后立即返回;一艘快艇在轮船出发2小时后从乙港出发,逆流航行2小时到达甲港,并立即返回(掉头时间忽略不计).已知水流的速度是1千米/米.如图表示轮船和快艇距甲港的距离y(千米)与轮船出发时间x(小时)之间的函数关系图象.
甲、乙两个港口相距36千米,一艘轮船从甲港出发,顺流航行3小时到达乙港.休息1小时后立即返回;一艘快艇在轮船出发2小时后从乙港出发,逆流航行2小时到达甲港,并立即返回(掉头时间忽略不计).已知水流的速度是1千米/米.如图表示轮船和快艇距甲港的距离y(千米)与轮船出发时间x(小时)之间的函数关系图象.(1)求轮船和快艇返回时的解析式,并写出自变量的取值范围;
(2)快艇出发多长时间,轮船和快艇在返回途中相距6千米?
分析:(1)先根据图象求出甲船的顺流速度,就可以由条件求出逆流航行速度,从求出轮船从乙港返回甲港的时间,就可以求出C的坐标,根据待定系数法就可以求出BC的解析式,同理先求出快艇的逆流速度,再根据条件可以求出顺流速度,从而可以快艇返回的时间,求出F的坐标.由待定系数法求出其解析式;
(2)根据(1)的解析式建立方程就可以得出结论.
(2)根据(1)的解析式建立方程就可以得出结论.
解答:解:(1)由题意,得
轮船顺水航行的速度为:36÷3=12km/时,
∴轮船逆流航行的速度为:12-1=11km/时.
∴轮船逆流航行的时间为:36÷11=
,
∴C(
,0)
快艇逆水航行的速度为:36÷2=18km/时,
∴快艇顺水航行的速度为:18+1=19km/时,
∴快艇顺水航行的时间为:
,
∴F(
,36).
设BC的解析式为y=k1x+b1,设EF的解析式为y=k2x+b2,由题意,得
,
,
解得:
,
,
BC的解析式为y1=-11x+80(4≤x≤
),
EF的解析式为y2=19x-76(4≤x≤
),
(2)由题意,得
y1-y2=±6,
当-11x+80-(19x-76)=6时,
解得:x=5,
当-11x+80-(19x-76)=-6时,
解得x=5.4
∴快艇出发3小时或5.4小时,轮船和快艇在返回途中相距6千米.
轮船顺水航行的速度为:36÷3=12km/时,
∴轮船逆流航行的速度为:12-1=11km/时.
∴轮船逆流航行的时间为:36÷11=
| 36 |
| 11 |
∴C(
| 80 |
| 11 |
快艇逆水航行的速度为:36÷2=18km/时,
∴快艇顺水航行的速度为:18+1=19km/时,
∴快艇顺水航行的时间为:
| 36 |
| 19 |
∴F(
| 112 |
| 19 |
设BC的解析式为y=k1x+b1,设EF的解析式为y=k2x+b2,由题意,得
|
|
解得:
|
|
BC的解析式为y1=-11x+80(4≤x≤
| 80 |
| 11 |
EF的解析式为y2=19x-76(4≤x≤
| 112 |
| 19 |
(2)由题意,得
y1-y2=±6,
当-11x+80-(19x-76)=6时,
解得:x=5,
当-11x+80-(19x-76)=-6时,
解得x=5.4
∴快艇出发3小时或5.4小时,轮船和快艇在返回途中相距6千米.
点评:本题是一道一次函数的综合试题,考查了航行问题在实际问题中的运用,待定系数法求一次函数的解析式的运用,解答时求出一次函数的解析式时解答本题的关键.

练习册系列答案
相关题目

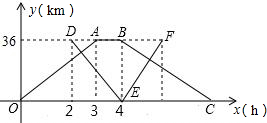 甲、乙两个港口相距36千米,一艘轮船从甲港出发,顺流航行3小时到达乙港.休息1小时后立即返回;一艘快艇在轮船出发2小时后从乙港出发,逆流航行2小时到达甲港,并立即返回(掉头时间忽略不计).已知水流的速度是1千米/米.如图表示轮船和快艇距甲港的距离y(千米)与轮船出发时间x(小时)之间的函数关系图象.
甲、乙两个港口相距36千米,一艘轮船从甲港出发,顺流航行3小时到达乙港.休息1小时后立即返回;一艘快艇在轮船出发2小时后从乙港出发,逆流航行2小时到达甲港,并立即返回(掉头时间忽略不计).已知水流的速度是1千米/米.如图表示轮船和快艇距甲港的距离y(千米)与轮船出发时间x(小时)之间的函数关系图象.
 速度是______千米/时;
速度是______千米/时;