题目内容
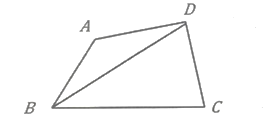
【题目】如图，有一形状为直角三角形的空地ABC，
，
，
，现要作一条垂直于斜边AB的小道
点E在斜边上，点F在直角边上
设
，
的面积为y．
求y与x的函数关系式
写出自变量x的取值范围
；
当x为何值时y有最大值？并求出最大值．
【答案】（1）
，
；（2）
时，y有最大值，最大值为
．
【解析】
过C作
于D，分两种情况讨论：当点F在AC上时，当点F在BC上时，分别依据相似三角形的对应边成比例可得EF的表达式，进而得出y与x的函数关系式；
根据二次函数的性质，即可得到当时，y有最大值．
由
，可得：
，如图所示，过C作于D，则
．分两种情况讨论：①当点F在AC上时，
∽
；
②当点F在BC上时，
∽
．
由
，可得当
时，y有最大值，最大值为216；
由
，可得当时，y有最大值，最大值为；
综上所述：当时，y有最大值，最大值为．
练习册系列答案
相关题目
