题目内容
函数y=
+
中,自变量x的取值范围是
| x+4 |
| 2-x |
-4≤x≤2
-4≤x≤2
.分析:根据被开方数大于等于0列式进行计算即可求解.
解答:解:根据题意得,x+4≥0,2-x≥0,
解得x≥-4,x≤2,
故自变量x的取值范围是-4≤x≤2.
故答案为:-4≤x≤2.
解得x≥-4,x≤2,
故自变量x的取值范围是-4≤x≤2.
故答案为:-4≤x≤2.
点评:本题考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
相关题目
函数y=
中自变量x的取值范围是( )
| ||
| x |
A、x≤
| ||
B、x>-
| ||
| C、x≠0 | ||
D、x<
|
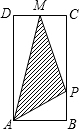 如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A?B?C?M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的( )
如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A?B?C?M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的( )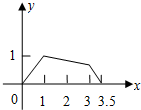


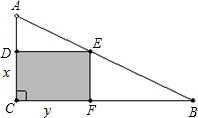 为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池.
为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池.