题目内容
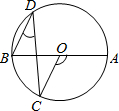如图，AB是⊙O直径，∠AOC=130°，则∠D=________°．
25
分析：由AB是⊙O直径，∠AOC=130°，根据邻补角的定义，即可求得∠BOC的度数，然后根据在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得∠D的度数．
解答：∵AB是⊙O直径，∠AOC=130°，
∴∠BOC=180°-∠AOC=50°，
∴∠D=
∠BOC=25°．
故答案为：25．
点评：此题考查了圆周角定理．此题比较简单，解题的关键是掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用．
分析：由AB是⊙O直径，∠AOC=130°，根据邻补角的定义，即可求得∠BOC的度数，然后根据在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得∠D的度数．
解答：∵AB是⊙O直径，∠AOC=130°，
∴∠BOC=180°-∠AOC=50°，
∴∠D=
∠BOC=25°．故答案为：25．
点评：此题考查了圆周角定理．此题比较简单，解题的关键是掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用．
练习册系列答案
相关题目
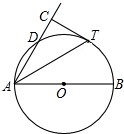如图，AB是⊙O直径，D为⊙O上一点，AT平分∠BAD交⊙O于点T，过T作AD的垂线交AD的延长线于点C．
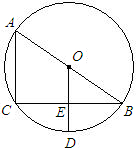如图，AB是⊙O直径，BC是弦，OD⊥BC于E交弧BC于D．根据中考改编
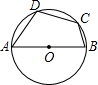如图，AB是⊙O直径，C、D是⊙O上的两点，若∠BAC=20°，
如图，AB是⊙O直径，OB=6，弦CD=10，则弦心距OP的长为（ ）
如图，AB是⊙O直径，弦CD交AB于E，∠AEC=45°，AB=2．设AE=x，CE2+DE2=y．下列图象中，能表示y与x的函数关系是的（ ）