题目内容
如图,已知直线l与y轴、x轴交于点A(0,8)、B(6,0)两点,直线 与y轴、直线l分别交于点C、D,求△ACD绕y轴旋转一周所围成几何体的表面积。
与y轴、直线l分别交于点C、D,求△ACD绕y轴旋转一周所围成几何体的表面积。

【答案】
3( +5)π.
+5)π.
【解析】
试题分析:应用待定系数法求出直线l的解析式,从而求出直线l与y轴交点坐标,联立直线l与直线 求出点D的坐标,根据线段AD、CD绕y轴旋转一轴所围成几何体是两个三棱锥组成求出其表面积.
求出点D的坐标,根据线段AD、CD绕y轴旋转一轴所围成几何体是两个三棱锥组成求出其表面积.
试题解析:设直线l的解析式为 ,
,
∵l与y轴、x轴交于A(0,8),B(6,0)两点,∴ ,解得
,解得 .∴直线l的解析式为
.∴直线l的解析式为 .
.
∵直线l与y轴交点为C,∴C(0,  8).
8).
∵直线l与直线 的交点为D,∴
的交点为D,∴ ,解得
,解得 .∴D(3,4).
.∴D(3,4).
线段AD、CD绕y轴旋转一轴所围成几何体是两个三棱锥组成.
∵D(3,4),C(0,-8),∴AD=5,CD=
∴AD为母线三棱锥的表面积:πrl=15π,CD为母线三棱锥的表面积:πrl= π.
π.
∴围成几何体的表面积=3( +5)π.
+5)π.
考点:1.待定系数法的应用;2.直线上点的坐标与方程的关系;3.旋转的性质;4. 三棱锥的表面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 26、如图,已知直线AB与CD相交于点O,OB平分∠EOD,∠1+∠2=90°,
26、如图,已知直线AB与CD相交于点O,OB平分∠EOD,∠1+∠2=90°,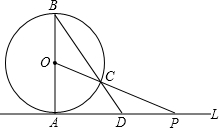 (1)若AP=4,求线段PC的长;
(1)若AP=4,求线段PC的长; 如图,已知直线AB与CD相交于点O,OE、OF分别是∠BOD、∠AOD的平分线.
如图,已知直线AB与CD相交于点O,OE、OF分别是∠BOD、∠AOD的平分线. 如图,已知直线l1与l2交于一点P,l1的函数表达式是y=2x+3,l2的函数表达式是y=kx+b(k≠0).点P的横坐标是-1,且l2与y轴的交点A的纵坐标也是-1.
如图,已知直线l1与l2交于一点P,l1的函数表达式是y=2x+3,l2的函数表达式是y=kx+b(k≠0).点P的横坐标是-1,且l2与y轴的交点A的纵坐标也是-1.