题目内容
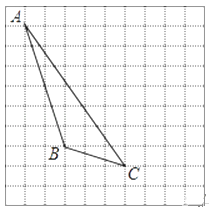
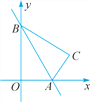
【题目】如图, 一次函数的图象与x轴,y轴分别相交于点A,B,将△AOB沿直线AB翻折,得△ACB.若点C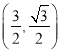 ,求该一次函数的表达式.
,求该一次函数的表达式.
【答案】y=-![]() x+
x+![]()
【解析】试题分析:求一次函数表达式,需要列两个方程.由C点坐标,利用勾股定理可以得到AC的长,AC=OA,也就得到了,A点坐标,得到第一个方程,同时,可以得到
∠ACM=30°,所以,∠ABO=30°易得B点坐标,得到第二个方程,也就可以求出一次函数的表达式.
如图,过点C作CM⊥x轴于点M,CN⊥y轴于点N.
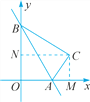
∵点C ,∴OM=NC=
,∴OM=NC=![]() ,ON=MC=
,ON=MC=![]() .
.
∵将△AOB沿直线AB翻折得到△ACB,∴OA=CA,OB=CB.
在Rt△CAM中,由勾股定理,得AC2=AM2+MC2,即OA2=(OM-OA)2+MC2,
∴OA2=![]() +
+![]() ,解得OA=1.
,解得OA=1.
∴点A(1,0).∴∠ACM=30°,∴∠ABO=30°,AB=2,∴OB=![]() ,点B(0,
,点B(0, ![]() ).
).
设直线AB的函数表达式为y=kx+b.
把点A,B的坐标代入,得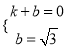 ,解得
,解得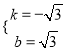
∴直线AB的函数表达式为y=-![]() x+
x+![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目